 |
Quick description
This is not a trick so much as a heuristic that allows one to not get too distracted with the unimportant components of an oscillatory integral (such as amplitude), and instead focus on the important components (namely, the geometry of the oscillation).
When controlling an oscillatory integral such as 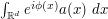 , the exact choice of amplitude function
, the exact choice of amplitude function 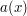 is rarely significant, so long as it is uniformly smooth with respect to all parameters of interest; one can often replace this amplitude function with another amplitude function
is rarely significant, so long as it is uniformly smooth with respect to all parameters of interest; one can often replace this amplitude function with another amplitude function 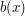 so long as
so long as  and
and 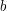 have similar behaviour at the stationary points
have similar behaviour at the stationary points 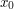 of
of 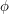 (e.g.
(e.g. 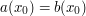 ).
).
A corollary of this is that any smooth perturbation of the phase 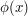 by a bounded correction
by a bounded correction 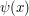 , thus replacing
, thus replacing 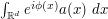 with
with 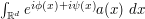 should lead to an extremely similar integral. Thus, as a first approximation, any component of the phase
should lead to an extremely similar integral. Thus, as a first approximation, any component of the phase 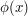 which is both smooth and bounded can (heuristically, at least) be dropped for the purposes of trying to predict what the behavior of this integral should be.
which is both smooth and bounded can (heuristically, at least) be dropped for the purposes of trying to predict what the behavior of this integral should be.
Prerequisites
Harmonic analysis
Example 1
Suppose one wishes to estimate the integral 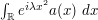 for some test function
for some test function 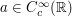 and some large parameter
and some large parameter 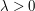 . One can replace the cutoff function
. One can replace the cutoff function 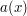 here by the more explicit function
here by the more explicit function 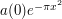 (which agrees with
(which agrees with  at the stationary point
at the stationary point 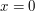 ), plus an error which vanishes at the stationary point. Computing the first term explicitly and bounding the second term via integration by parts, one obtains an asymptotic for this integral, namely
), plus an error which vanishes at the stationary point. Computing the first term explicitly and bounding the second term via integration by parts, one obtains an asymptotic for this integral, namely 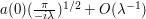 ; see "linearize the phase" for further discussion.
; see "linearize the phase" for further discussion.
General discussion
Other examples of this general heuristic appear in "How to use the method of stationary phase to control oscillatory integrals".
See also "Getting rid of nasty cutoffs".
 Tricki
Tricki
Comments
Post new comment
(Note: commenting is not possible on this snapshot.)