Quick description
The method of stationary phase is a collection of techniques used to estimate oscillatory integrals such as

where  is a smooth bump function,
is a smooth bump function, 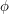 is a smooth real-valued phase function, and
is a smooth real-valued phase function, and 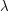 is a large real parameter. In many cases (particularly if the stationary points of the phase
is a large real parameter. In many cases (particularly if the stationary points of the phase 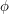 are isolated and non-degenerate), the methods give not only upper bounds, but a full asymptotic expansion of such integrals.
are isolated and non-degenerate), the methods give not only upper bounds, but a full asymptotic expansion of such integrals.
There are three main pillars of the theory:
-
Localization (the principle of non-stationary phase) If
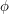 is non-stationary (i.e.
is non-stationary (i.e. 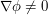 ) on the support of
) on the support of  , then the integral decays very rapidly in
, then the integral decays very rapidly in 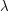 (faster than any power of
(faster than any power of 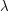 ). This is proven by repeated integration by parts or by linearizing the phase. As a consequence, oscillatory integrals can often be localised to individual stationary points, particularly if such points are isolated.
). This is proven by repeated integration by parts or by linearizing the phase. As a consequence, oscillatory integrals can often be localised to individual stationary points, particularly if such points are isolated.
-
Scaling The magnitude of an oscillatory integral around a stationary point decays at a rate determined by the order of stationarity (or more precisely, on the Newton polytope of the phase at a stationary point). One manifestation of this is the van der Corput lemma for oscillatory integrals.
-
Asymptotics If the phase is stationary and non-degenerate at a point, then one can perform a change of variables (using Morse theory) to place the phase in a canonical form, e.g. a diagonal quadratic form. This allows one to create asymptotic expansions for the integral around each such stationary point.
If all one is seeking is upper bounds on an integral such as 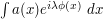 , and one is fortunate enough to have only one stationary point
, and one is fortunate enough to have only one stationary point 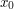 (i.e. only one solution to the equation
(i.e. only one solution to the equation 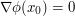 , then a "quick and dirty" heuristic for "right" upper bound for this integral is this: the integral should be bounded by the amplitude
, then a "quick and dirty" heuristic for "right" upper bound for this integral is this: the integral should be bounded by the amplitude 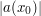 at the stationary point
at the stationary point 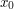 , times the volume of the region
, times the volume of the region 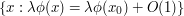 near the point of stationary phase where the phase does not oscillate. (This can be viewed as a non-rigorous, oscillatory version of the base times height heuristic.)
near the point of stationary phase where the phase does not oscillate. (This can be viewed as a non-rigorous, oscillatory version of the base times height heuristic.)
Prerequisites
Harmonic analysis
Example 1
Problem (Fresnel-type integral) Let 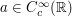 be a compactly supported bump function that is non-vanishing at the origin. Obtain as good an upper bound as one can on the magnitude of the integral
be a compactly supported bump function that is non-vanishing at the origin. Obtain as good an upper bound as one can on the magnitude of the integral 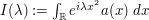 as a function of
as a function of 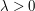 . [For sake of discussion, let's not keep track of the dependence on
. [For sake of discussion, let's not keep track of the dependence on  .]
.]
Solution The base times height bound gives a crude upper bound of 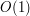 . When
. When 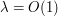 , the phase
, the phase 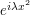 only undergoes a bounded number of oscillations across the compact support of
only undergoes a bounded number of oscillations across the compact support of  , so one does not expect any significant improvement to this
, so one does not expect any significant improvement to this 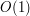 bound except when
bound except when 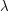 is large. So now we will assume that
is large. So now we will assume that 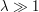 .
.
The phase  is stationary at
is stationary at 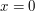 . Starting at this stationary point and then moving
. Starting at this stationary point and then moving  away from this point, we see that
away from this point, we see that 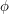 reaches its first full oscillation (i.e.
reaches its first full oscillation (i.e. 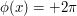 or
or 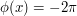 ) when
) when  is comparable to
is comparable to 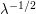 . After that, it oscillates more and more rapidly, with the wavelengths becoming significantly smaller than
. After that, it oscillates more and more rapidly, with the wavelengths becoming significantly smaller than 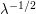 as one moves away from the origin. So the "base" of this oscillatory integral is of size about
as one moves away from the origin. So the "base" of this oscillatory integral is of size about 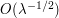 , while the "height" is
, while the "height" is 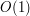 , leading to a prediction of
, leading to a prediction of 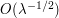 .
.
To make this argument more precise, what one can do is perform a smooth dyadic partition of unity to decompose the bump function  to a bump function
to a bump function 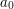 supported on the region
supported on the region 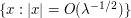 , plus a telescoping sum of bump functions
, plus a telescoping sum of bump functions 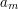 supported on the dyadic annuli
supported on the dyadic annuli 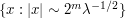 , where
, where 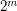 ranges between
ranges between  and
and 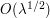 .
.
Let's first consider the main term 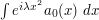 . Here, there is no significant oscillation and one should apply the base times height bound, which gives a contribution of
. Here, there is no significant oscillation and one should apply the base times height bound, which gives a contribution of 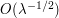 for this term.
for this term.
Now let's look at one of the auxiliary terms 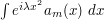 . On the region of integration
. On the region of integration 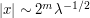 , the phase
, the phase  is oscillating at a rate
is oscillating at a rate 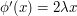 , which is about
, which is about 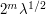 in magnitude; in other words, the phase has a wavelength of about
in magnitude; in other words, the phase has a wavelength of about 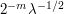 . In contrast, the width of the cutoff function
. In contrast, the width of the cutoff function 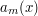 is about
is about 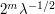 . Since the phase is oscillating faster than the cutoff, there is an opportunity to use integration by parts to exploit cancellation. Indeed, if we write this expression as
. Since the phase is oscillating faster than the cutoff, there is an opportunity to use integration by parts to exploit cancellation. Indeed, if we write this expression as
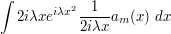
and integrate by parts, one obtains
![- \int e^{i \lambda x} \frac{d}{dx} [ \frac{1}{2 i \lambda x} a_m(x) ]\ dx.](../images/tex/eb4bc076e8e7390ccfd03b29331297a0.png)
Computing the derivative ![\frac{d}{dx} [ \frac{1}{2 i \lambda x} a_m(x) ]](../images/tex/b6b882af3c9483644ffec19a70853179.png) , one sees that the dominant term is
, one sees that the dominant term is 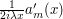 , which has size about
, which has size about 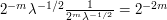 . Applying the base times height bound, we thus see that this integral has a size of about
. Applying the base times height bound, we thus see that this integral has a size of about 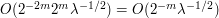 . (Actually, one could repeatedly integrate by parts here and get even better decay in
. (Actually, one could repeatedly integrate by parts here and get even better decay in  , but this is already enough decay to sum the series.) Summing in
, but this is already enough decay to sum the series.) Summing in  , one obtains the desired bound of
, one obtains the desired bound of 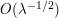 for
for 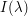 .
.
The same analysis shows that if the amplitude function  vanishes to some order
vanishes to some order  at the origin, then one obtains a bound of
at the origin, then one obtains a bound of 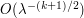 for the integral
for the integral 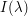 . The same is true if we take
. The same is true if we take  to be a Schwartz function rather than a bump function. Thus, to obtain asymptotics for
to be a Schwartz function rather than a bump function. Thus, to obtain asymptotics for 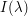 (not just upper bounds), up to an error of
(not just upper bounds), up to an error of 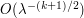 , one can replace
, one can replace  with some concrete Schwartz function approximant which agrees with
with some concrete Schwartz function approximant which agrees with  to
to 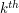 order at the origin, e.g. a polynomial times the gaussian
order at the origin, e.g. a polynomial times the gaussian 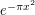 . If one does this, one can get a full asymptotic expansion for
. If one does this, one can get a full asymptotic expansion for 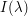 ; see "linearize the phase" for the derivation of the first term of this expansion.
; see "linearize the phase" for the derivation of the first term of this expansion.
Example 2
Problem: (Frequency-localized fundamental solution for the Schrodinger equation) Obtain as good a bound as one can for the magnitude of the expression 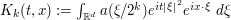 , where
, where  is an integer,
is an integer, 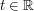 ,
, 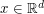 , and
, and  is a bump function supported on the annulus
is a bump function supported on the annulus 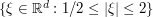 . [For sake of discussion, let's not keep track of the dependence of constants on
. [For sake of discussion, let's not keep track of the dependence of constants on 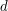 and
and  ; the goal is to get the optimal dependence on
; the goal is to get the optimal dependence on 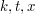 .]
.]
Solution: Firstly, we normalize parameters by performing the change of variables 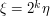 , giving
, giving
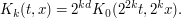
Thus, it suffices to handle the case 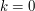 , as we can then get bounds for the other
, as we can then get bounds for the other  by substitution. We are now trying to bound
by substitution. We are now trying to bound
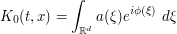
where 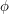 is the phase
is the phase
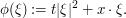
The base times height bound gives an upper bound of 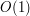 . To do better, we look at the gradient of the phase:
. To do better, we look at the gradient of the phase:
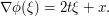
Thus we see that we have just one stationary point, at 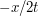 , except when
, except when 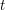 degenerates to zero.
degenerates to zero.
Let's deal with the degenerate case first. When 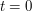 , we just have a Fourier integral of a bump function; in addition to the trivial bound of
, we just have a Fourier integral of a bump function; in addition to the trivial bound of 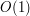 , we will have a bound of
, we will have a bound of 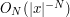 for any
for any 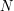 by repeated integration by parts, so the correct bound here is
by repeated integration by parts, so the correct bound here is  (where we write
(where we write  ). A similar argument also handles the case when
). A similar argument also handles the case when 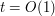 ; indeed, in such cases we can simply absorb the
; indeed, in such cases we can simply absorb the 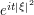 phase into the bump function
phase into the bump function 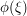 and still get a bump function.
and still get a bump function.
Now let's look at the non-degenerate case, when 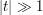 . If
. If 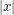 is much larger than
is much larger than  , e.g.
, e.g. 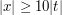 , then the gradient of the phase is always at least
, then the gradient of the phase is always at least 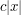 for some absolute constant
for some absolute constant  , so by repeated integration by parts we see that we can get a bound of
, so by repeated integration by parts we see that we can get a bound of 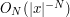 in this case. Similarly, if
in this case. Similarly, if  is much smaller than
is much smaller than 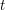 , e.g.
, e.g. 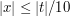 , then the gradient of the phase is always at least
, then the gradient of the phase is always at least 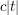 , so by repeated integration by parts we can get a bound of
, so by repeated integration by parts we can get a bound of 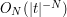 in this case.
in this case.
The remaining case is when 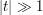 and
and 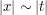 . Here, we expect the stationary point to lie inside the support of
. Here, we expect the stationary point to lie inside the support of  and so we longer get arbitrary amounts of decay. But we can now use stationary phase. First let's work heuristically: at the stationary point
and so we longer get arbitrary amounts of decay. But we can now use stationary phase. First let's work heuristically: at the stationary point 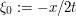 , we have
, we have 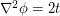 , so we can Taylor expand
, so we can Taylor expand 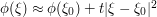 . (In fact, this expansion happens to be exact in this case - by completing the square - but we will not exploit this.) Thus, we see that the stationary region
. (In fact, this expansion happens to be exact in this case - by completing the square - but we will not exploit this.) Thus, we see that the stationary region 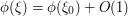 consists of those
consists of those 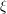 for which
for which 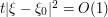 , which is a ball of radius
, which is a ball of radius 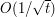 centred at
centred at 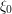 . This ball has volume
. This ball has volume 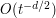 , and the amplitude function
, and the amplitude function 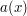 has height
has height 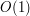 , so by base times height we expect a bound here of
, so by base times height we expect a bound here of 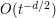 .
.
One can justify this heuristic by off-the-shelf stationary phase estimates. For instance, one can rewrite the integral as
![\int_{\R^d} a(\xi) e^{i t [ |\xi|^2 + \frac{x}{t} \cdot \xi ]}\ d\xi](../images/tex/4d77e10e0c2b96ec181b116724e5066f.png)
and apply stationary phase with 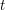 being the asymptotic parameter and
being the asymptotic parameter and 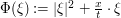 being the phase; since we are restricting to the region
being the phase; since we are restricting to the region 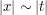 , the phase is uniformly smooth and so the constants arising from the stationary phase bounds will not have any further dependence on
, the phase is uniformly smooth and so the constants arising from the stationary phase bounds will not have any further dependence on 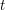 .
.
Putting everything together, we obtain the following bounds on 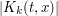 , which turn out to be basically optimal:
, which turn out to be basically optimal:
-
A bound of
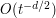 when
when 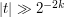 and
and 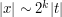 ;
; -
A bound of
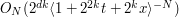 for any
for any 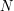 otherwise.
otherwise.
With more work, one can get asymptotics for these integrals, not just upper bounds.
Example 3
Problem: (Frequency-localized fundamental solution for the wave equation) Obtain as good a bound as one can for the magnitude of the expression 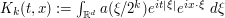 , where
, where  is an integer,
is an integer, 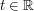 ,
, 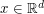 , and
, and  is a bump function supported on the annulus
is a bump function supported on the annulus 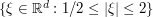 .
.
Solution: Again we can rescale 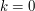 ; this time, the scaling relation is given as
; this time, the scaling relation is given as
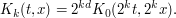
It is also convenient to exploit some more symmetries: we can flip 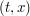 to
to 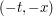 at the expense of conjugating
at the expense of conjugating 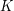 , so can normalize
, so can normalize 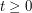 ; similarly, the integral is unchanged under rotation of
; similarly, the integral is unchanged under rotation of  , so we may assume
, so we may assume  is oriented along the
is oriented along the 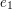 direction, thus
direction, thus  for some
for some 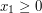 .
.
So now we look for upper bounds of 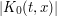 . As before, when
. As before, when 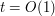 we obtain the bounds of
we obtain the bounds of 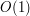 from base times height, and
from base times height, and 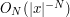 from repeated integration by parts, leading to a net bound of
from repeated integration by parts, leading to a net bound of  in this case.
in this case.
Now take 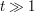 . Here, the derivative of the phase
. Here, the derivative of the phase 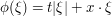 is
is
so a stationary point will now occur along a ray 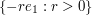 if
if 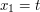 , and no stationary point will occur otherwise.
, and no stationary point will occur otherwise.
We can dispose of an easy case when 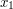 is large, e.g.
is large, e.g. 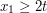 . Here the phase has gradient at least
. Here the phase has gradient at least 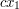 everywhere for some
everywhere for some 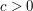 , and repeated integration by parts gives the bound
, and repeated integration by parts gives the bound  . Similarly, when
. Similarly, when 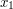 is small, e.g.
is small, e.g. 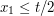 , the gradient is at least
, the gradient is at least 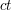 everywhere, and repeated integration by parts gives the bound
everywhere, and repeated integration by parts gives the bound 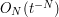 . So we may assume that
. So we may assume that 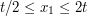 .
.
We know that the ray 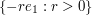 is going to be the most dangerous region, so we now try to localize there. We thus write
is going to be the most dangerous region, so we now try to localize there. We thus write 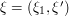 where
where 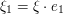 and
and 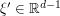 . In the region where
. In the region where 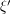 is large, e.g.
is large, e.g. 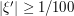 , or when
, or when 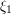 is not large and negative, e.g.
is not large and negative, e.g. 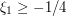 , the gradient of the phase
, the gradient of the phase 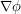 is at least
is at least 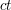 by (1), and by smoothly truncating to this portion of the domain of integration we see that the contribution here is
by (1), and by smoothly truncating to this portion of the domain of integration we see that the contribution here is 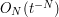 . So now let us localize to the remaining portion, where
. So now let us localize to the remaining portion, where 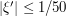 and
and 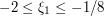 , say (the exact numerical values here are not important).
, say (the exact numerical values here are not important).
At this point, it can clarify things heuristically to try to linearize the phase. As 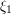 is large and
is large and 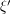 is small, we can Taylor expand
is small, we can Taylor expand
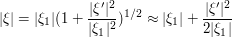
where we use the approximation  . Thus the phase is roughly of the form
. Thus the phase is roughly of the form
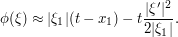
This expansion highlights the fact that the phase 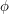 is at its most stationary when
is at its most stationary when 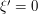 and
and 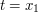 .
.
Let's first handle the extreme case 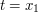 . Here, the phase is indeed stationary at
. Here, the phase is indeed stationary at 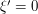 (where it is zero), and the stationary region is basically the cylinder where
(where it is zero), and the stationary region is basically the cylinder where 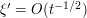 . This cylinder has volume
. This cylinder has volume 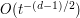 , so this would heuristically be the bound for the integral in this case. To do this rigorously (and using the original phase, rather than the heuristic approximation to this phase), one can perform (smooth) dyadic decomposition to this cylinder, plus the remaining cylinders
, so this would heuristically be the bound for the integral in this case. To do this rigorously (and using the original phase, rather than the heuristic approximation to this phase), one can perform (smooth) dyadic decomposition to this cylinder, plus the remaining cylinders 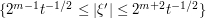 . The original cylinder yields a contribution of
. The original cylinder yields a contribution of 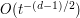 by the base times height bound. On the remaining cylinders, there is some non-trivial oscillation in the
by the base times height bound. On the remaining cylinders, there is some non-trivial oscillation in the 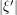 direction; exploiting that by repeated integration by parts, we eventually see that the contribution of the
direction; exploiting that by repeated integration by parts, we eventually see that the contribution of the 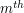 cylinder is
cylinder is 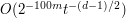 (say), so on summing we do get
(say), so on summing we do get 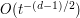 as claimed.
as claimed.
Now we can handle the general case 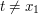 . This is as before, but now there is also some oscillation along the
. This is as before, but now there is also some oscillation along the 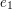 axis as well as in the
axis as well as in the 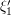 direction. For instance, in the cylinder
direction. For instance, in the cylinder 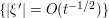 , we can improve upon the trivial bound of
, we can improve upon the trivial bound of 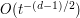 to obtain
to obtain 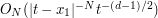 for any
for any 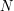 , and similarly for the other cylinders, to on summing we now get a net bound of
, and similarly for the other cylinders, to on summing we now get a net bound of 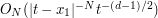 .
.
Putting all this together, we get the bounds
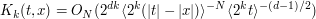
for all 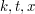 .
.
Example 4
Problem: (Frequency-localized fundamental solution for the Klein-Gordon equation) Obtain as good a bound as one can for the magnitude of the expression 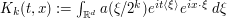 , where
, where  is an integer,
is an integer, 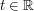 ,
, 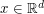 , and
, and  is a bump function supported on the annulus
is a bump function supported on the annulus 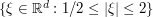 .
.
Solution: This is a particularly tricky one, requiring quite a few computations and cases.
Once again, we try to rescale 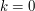 . But this time, we run into a hitch: the phase
. But this time, we run into a hitch: the phase 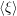 is not scale-invariant, so we cannot eliminate
is not scale-invariant, so we cannot eliminate  completely. Instead, we get
completely. Instead, we get
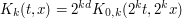
where
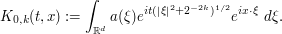
As before, we can exploit some symmetries and reduce to the case 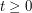 and
and  for some
for some 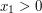 .
.
If we first look at the limit 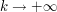 , we see that this integral collapses to the integral considered in the preceding exercise. At the other extreme
, we see that this integral collapses to the integral considered in the preceding exercise. At the other extreme 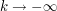 , we have a Taylor expansion
, we have a Taylor expansion
and the situation begins to more closely resemble the Schrodinger example. So it looks like we may have to divide into cases, with large  behaving like the wave equation, and small
behaving like the wave equation, and small  behaving like the Schrodinger equation.
behaving like the Schrodinger equation.
The case  can in fact be handled by the Schrodinger methods without much difficulty. Guided by the approximation (2), we can write
can in fact be handled by the Schrodinger methods without much difficulty. Guided by the approximation (2), we can write
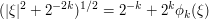
and one checks that 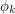 is smooth on the support of
is smooth on the support of  uniformly for
uniformly for  , and furthermore
, and furthermore 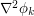 is uniformly non-degenerate. Off-the-shelf stationary phase tools then give the bound
is uniformly non-degenerate. Off-the-shelf stationary phase tools then give the bound 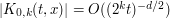 if
if 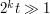 and
and 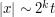 , and
, and 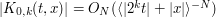 for any
for any 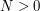 otherwise.
otherwise.
Now let's look at the case when 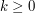 . As before, we get a bound of
. As before, we get a bound of  when
when 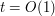 , so suppose
, so suppose 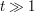 .
.
The gradient of the phase 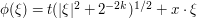 is
is
As in the wave case, we can then use repeated integration by parts to obtain a decay of  when
when 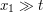 and
and 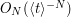 when
when 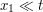 , so we can restrict attention to the case when
, so we can restrict attention to the case when 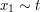 .
.
We expect the phase to be stationary near the negative 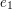 axis, so we try Taylor expansion around that ray. Writing
axis, so we try Taylor expansion around that ray. Writing 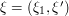 as before, we obtain
as before, we obtain
In the case when  , the term
, the term 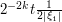 is of bounded size, and so we do not expect this term to contribute much to the bounds. In other words, in this case the bounds should be the same as those for the wave equation, namely
is of bounded size, and so we do not expect this term to contribute much to the bounds. In other words, in this case the bounds should be the same as those for the wave equation, namely 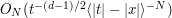 for any
for any 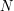 . And indeed, one can check that the arguments in the previous exercise can be repeated in this range of
. And indeed, one can check that the arguments in the previous exercise can be repeated in this range of 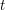 to give the stated bound.
to give the stated bound.
Finally, we look at the case when 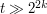 . If
. If 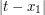 is much larger than
is much larger than 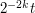 , then the phase oscillation from the
, then the phase oscillation from the 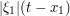 term is greater than that from the
term is greater than that from the 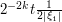 term, so the wave equation arguments will still give a bound of
term, so the wave equation arguments will still give a bound of 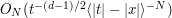 .
.
If instead 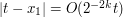 , then the portion
, then the portion 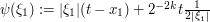 of the (Taylor approximation of the) phase will have a stationary point, with a second derivative of roughly
of the (Taylor approximation of the) phase will have a stationary point, with a second derivative of roughly 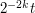 . From the approximation (4), we thus expect the stationary region to have size about
. From the approximation (4), we thus expect the stationary region to have size about 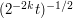 in the
in the 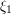 direction and
direction and 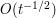 in the other directions, leading to a prediction of
in the other directions, leading to a prediction of 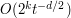 for the size of the integral. This can be made rigorous by first dividing the region of integration into cylinders as in the previous example (i.e. smoothly partitioning the
for the size of the integral. This can be made rigorous by first dividing the region of integration into cylinders as in the previous example (i.e. smoothly partitioning the 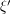 variable around the critical value
variable around the critical value 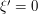 ), and then partitioning those cylinders further in the
), and then partitioning those cylinders further in the 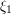 direction, based on the stationary point indicated in (3). We omit the rather tedious computations, and instead just give the final bounds for
direction, based on the stationary point indicated in (3). We omit the rather tedious computations, and instead just give the final bounds for 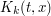 after putting all the above cases together, which are
after putting all the above cases together, which are
-
 if
if  ,
, 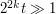 and
and 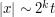 ;
; -
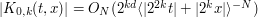 for any
for any 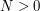 in all other cases with
in all other cases with  ;
; -
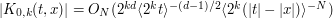 when
when 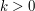 and
and 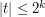 or
or  ;
; -
 if
if 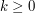 ,
, 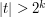 , and
, and 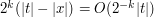 .
.
General discussion
The methods can be adapted to deal with more general amplitude functions 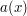 than bump functions by such tools as (smooth) dyadic decomposition.
than bump functions by such tools as (smooth) dyadic decomposition.
A good discussion of the technique can be found in Stein's book on harmonic analysis.
The more classical method of steepest descent, based on contour shifting, can also reproduce some of the results of stationary phase.
A variant of the base times height heuristic can give a means to predict the right order of magnitude of an oscillatory integral 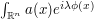 near a stationary point
near a stationary point 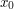 : the magnitude should roughly equal the "height"
: the magnitude should roughly equal the "height" 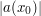 , times the size of the "base", defined as the set of points
, times the size of the "base", defined as the set of points  near
near 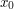 where
where 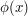 is within
is within 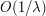 of
of 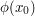 (i.e. the region near the stationary point
(i.e. the region near the stationary point 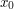 where phase has not yet begun to oscillate). For instance,
where phase has not yet begun to oscillate). For instance, 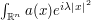 should be about
should be about 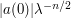 in magnitude.
in magnitude.
 Tricki
Tricki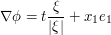
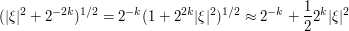
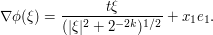
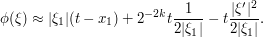
Comments
Title
Fri, 01/05/2009 - 16:31 — VickyIs there perhaps a more helpful title for this article? If you don't know what the method of stationary phase is, then it's entirely unclear what this article is about and which problems the method tackles!
Vicky, if you spot more of
Fri, 01/05/2009 - 18:23 — gowersVicky, if you spot more of those it would be great. I've just found one of my own: using the law of trichotomy. I'm about to change it to something more descriptive and imperative.
Fair enough
Sat, 02/05/2009 - 00:15 — taoI renamed it (and added another example, while I'm here...)
Post new comment
(Note: commenting is not possible on this snapshot.)