I am not completely sure about this. One could argue that proving convergence is not one of the global aims of mathematics (in the way that, say, classifying structures or proving nonequivalence are), but more like something that you often need to do when you are solving other problems. So perhaps an article about it should therefore appear somewhere a bit lower down the hierarchy, in an analysis page, say. What do others think about this?
Your thoughts on this are interesting. I would be curious to hear your argument on how proving convergence is not as fundamental a task in math as, say, how to optimize, or any other item in the `what kind of problem am i trying to solve?' page.
I would be curious to hear what others think on this as well. I disagree with Professor Gowers on many of his objections to my proposals and my writing. I feel I get involved in these personal discussions with him and it is not productive. So if others have opinions as well please let us hear them and I would be happy to go with the direction where most people feel like we should go.
My point of view on this issue is clear: convergence is a fundamental concept, it is logical to have an article on techniques to establish it with a link in `what kind of problem am i trying to solve?'
The reason I proposed a page like this was because I was writing two articles on proving convergence and I needed a parent article for them and the one I proposed sounded natural to me. The reason why my first post on this was so brief [with no arguments trying to justify my proposal] was because I thought this was a very obvious proposal.
I should make it clear that what I wrote was tentative: I don't have a definite view on this matter but wanted to argue that it was not obvious. Like you, I would much prefer it if others got involved in this discussion too.
But since it's just me at the moment, let me try to answer your question about which is more fundamental out of proving convergence and optimizing. The first thing to say is that I'm not sure that I would want to say that proving convergence is less fundamental. My view is more that it's less of a top-level objective. I could be wrong about this (which is why further feedback would be very useful) but it seems to me that there would be many more research papers with an abstract that says something like "We prove that the largest value of X is t" than with an abstract that says something like, "We prove that the following sequence converges." Somehow, proving convergence feels more like a means to an end rather than an end in itself.
I can think of possible exceptions. For example, it is a major problem to find a limiting model for a self-avoiding random walk, and it used to be a major problem to prove that the partial sums of the Fourier expansion of a function in converge almost everywhere.
So my previous message, and this one, were meant as a question. Is it better to have convergence right up there at the top level as one of the big general goals of mathematics, or is it better placed one level down – as one of the big general goals of analysis?
And many thanks for your work so far on the Tricki: I have opinions on things, of course, and would like to express them, and at this early stage I partly want to express them because if I don't then precedents may be set that I don't want to be set. But if others have different opinions, then they should express them too – I want to negotiate rather than dictate.
Thank you for your kind response. The tagging idea is great, as you said it would make tricki much more accessible.
Wouldn't putting all the techniques and ideas to study convergence under the title ``analysis'' be restrictive? For example, p-adic limits, would it be best to put techniques to establish it under analysis? There may be other concepts of convergence that come up in algebra, geometry, etc. And there can be general ideas/techniques which could be useful in thinking about any type of convergence in all of these fields.
> But why would that count as lower-level than *** / equals / *** ? I think
> perhaps because the word "converges" is quite a lot more specific and area
> dependent than the word "equals".
In the spirit of a conversation, and slightly independent of tricki, I would like to share some thoughts about convergence that relate to this thought you expressed.
I think that, in math, and in life, one very fundamental concept is that of refinement. We study [or in life observe] a class of objects and their relations etc. In our study we very often realize that these object can be broken into further pieces, or that our class of interest can be embedded into a larger class. And we further realize that this process can be repeated. As the refinement proceeds there is also an accompanying simplification. I think studying convergence is studying/quantifying this type of behavior.
Another related thought: understanding convergence is also good for classification. Seemingly disparate structures that arise in different fields are revealed to be related as we study certain limits.
I've thought of more to say on this topic. First of all, I agree that it makes perfect sense to have a single page called "Techniques for proving convergence" that could act as a parent for several articles on this general theme. The question in my mind is not whether that article should exist – it should – but what its parent should be.
My thoughts on the page What kind of problem am I trying to solve? have now become more specific, in that I think I have a slightly more objective way of explaining my instincts about it. They are connected with some extensive discussions I have had with Olof about a tagging system we hope to introduce that will describe articles by the problems they solve and the statements they treat. The idea is that eventually you would be able to type in something like this (with the / symbol denoting a division of the text into distinct units):
every / subgroup / of index 2 / of group / is / normal
and if there was a Tricki article that had tagged up this statement you would be led to it.
But you would also have the option of typing something like
every / subgroup / such that
and you might find yourself at a more general article entitled something like "Proving facts about subgroups".
Now if we can get a system like this going, then a page like "Techniques for proving existence" would show up very quickly, since all you'd have to type in would be
there exists /
So that is my semi-objective criterion. I feel that the navigation pages linked to from What kind of problem am I trying to solve? should be at this very high level. With that idea in mind, let me see how many of the existing articles I can "tag" at the top level:
Techniques for proving equalities and identities Hmm, my criterion seems to break down here: it genuinely feels like a fundamental task, but usually the nature of the task doesn't become clear at the very first word.
What about convergence? It seems to me that the right tag for a general page about convergence would be something like *** / converges / *** , where the *** denote wildcards that can be filled in in various ways. For instance one might have the statement
Every / sequence / in a / closed / bounded / interval / has a / subsequence / such that / subsequence / converges.
But why would that count as lower-level than *** / equals / *** ? I think perhaps because the word "converges" is quite a lot more specific and area-dependent than the word "equals".
Hmm ... I thought writing this was going to be easier than it has turned out to be.
Tricki
I vote yes!
I am not completely sure about this. One could argue that proving convergence is not one of the global aims of mathematics (in the way that, say, classifying structures or proving nonequivalence are), but more like something that you often need to do when you are solving other problems. So perhaps an article about it should therefore appear somewhere a bit lower down the hierarchy, in an analysis page, say. What do others think about this?
Also, it's already navigated to on the page I have a problem to solve in real analysis. Maybe that and the analysis front page would be enough.
Your thoughts on this are interesting. I would be curious to hear your argument on how proving convergence is not as fundamental a task in math as, say, how to optimize, or any other item in the `what kind of problem am i trying to solve?' page.
I would be curious to hear what others think on this as well. I disagree with Professor Gowers on many of his objections to my proposals and my writing. I feel I get involved in these personal discussions with him and it is not productive. So if others have opinions as well please let us hear them and I would be happy to go with the direction where most people feel like we should go.
My point of view on this issue is clear: convergence is a fundamental concept, it is logical to have an article on techniques to establish it with a link in `what kind of problem am i trying to solve?'
The reason I proposed a page like this was because I was writing two articles on proving convergence and I needed a parent article for them and the one I proposed sounded natural to me. The reason why my first post on this was so brief [with no arguments trying to justify my proposal] was because I thought this was a very obvious proposal.
I should make it clear that what I wrote was tentative: I don't have a definite view on this matter but wanted to argue that it was not obvious. Like you, I would much prefer it if others got involved in this discussion too.
But since it's just me at the moment, let me try to answer your question about which is more fundamental out of proving convergence and optimizing. The first thing to say is that I'm not sure that I would want to say that proving convergence is less fundamental. My view is more that it's less of a top-level objective. I could be wrong about this (which is why further feedback would be very useful) but it seems to me that there would be many more research papers with an abstract that says something like "We prove that the largest value of X is t" than with an abstract that says something like, "We prove that the following sequence converges." Somehow, proving convergence feels more like a means to an end rather than an end in itself.
I can think of possible exceptions. For example, it is a major problem to find a limiting model for a self-avoiding random walk, and it used to be a major problem to prove that the partial sums of the Fourier expansion of a function in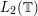
converge almost everywhere.
So my previous message, and this one, were meant as a question. Is it better to have convergence right up there at the top level as one of the big general goals of mathematics, or is it better placed one level down – as one of the big general goals of analysis?
And many thanks for your work so far on the Tricki: I have opinions on things, of course, and would like to express them, and at this early stage I partly want to express them because if I don't then precedents may be set that I don't want to be set. But if others have different opinions, then they should express them too – I want to negotiate rather than dictate.
Thank you for your kind response. The tagging idea is great, as you said it would make tricki much more accessible.
Wouldn't putting all the techniques and ideas to study convergence under the title ``analysis'' be restrictive? For example, p-adic limits, would it be best to put techniques to establish it under analysis? There may be other concepts of convergence that come up in algebra, geometry, etc. And there can be general ideas/techniques which could be useful in thinking about any type of convergence in all of these fields.
> But why would that count as lower-level than *** / equals / *** ? I think
> perhaps because the word "converges" is quite a lot more specific and area
> dependent than the word "equals".
In the spirit of a conversation, and slightly independent of tricki, I would like to share some thoughts about convergence that relate to this thought you expressed.
I think that, in math, and in life, one very fundamental concept is that of refinement. We study [or in life observe] a class of objects and their relations etc. In our study we very often realize that these object can be broken into further pieces, or that our class of interest can be embedded into a larger class. And we further realize that this process can be repeated. As the refinement proceeds there is also an accompanying simplification. I think studying convergence is studying/quantifying this type of behavior.
Another related thought: understanding convergence is also good for classification. Seemingly disparate structures that arise in different fields are revealed to be related as we study certain limits.
I've thought of more to say on this topic. First of all, I agree that it makes perfect sense to have a single page called "Techniques for proving convergence" that could act as a parent for several articles on this general theme. The question in my mind is not whether that article should exist – it should – but what its parent should be.
My thoughts on the page What kind of problem am I trying to solve? have now become more specific, in that I think I have a slightly more objective way of explaining my instincts about it. They are connected with some extensive discussions I have had with Olof about a tagging system we hope to introduce that will describe articles by the problems they solve and the statements they treat. The idea is that eventually you would be able to type in something like this (with the / symbol denoting a division of the text into distinct units):
every / subgroup / of index 2 / of group / is / normal
and if there was a Tricki article that had tagged up this statement you would be led to it.
But you would also have the option of typing something like
every / subgroup / such that
and you might find yourself at a more general article entitled something like "Proving facts about subgroups".
Now if we can get a system like this going, then a page like "Techniques for proving existence" would show up very quickly, since all you'd have to type in would be
there exists /
So that is my semi-objective criterion. I feel that the navigation pages linked to from What kind of problem am I trying to solve? should be at this very high level. With that idea in mind, let me see how many of the existing articles I can "tag" at the top level:
Techniques for finding algorithms and algorithmic proofs: this is not very easy to justify according to the above criterion, but perhaps "Find systematically" would do the job.
Techniques for classifying mathematical structures: "Classify"
Techniques for comparing sets and mathematical structures: not so easy to justify, which fits with my doubts about whether this category of problem belongs on this page.
Techniques for counting: "Count" or "How many"
Techniques for solving equations: "Solve"
Techniques for obtaining estimates: "Estimate"
Techniques for proving existence: "There exists"
Techniques for producing explicit examples: "Find / an explicit" again, not perfect, which perhaps explains why I was anxious about this one. Maybe it should be a subpage of Techniques for proving existence.
Techniques for proving equalities and identities Hmm, my criterion seems to break down here: it genuinely feels like a fundamental task, but usually the nature of the task doesn't become clear at the very first word.
Techniques for proving impossibility and nonexistence: "There is no"
Techniques for proving inequalities: a similar problem to the equalities and identities problem.
Techniques for maximizing and minimizing: "Maximize"
Techniques for proving "for all" statements: "Every" or "For every".
What about convergence? It seems to me that the right tag for a general page about convergence would be something like *** / converges / *** , where the *** denote wildcards that can be filled in in various ways. For instance one might have the statement
Every / sequence / in a / closed / bounded / interval / has a / subsequence / such that / subsequence / converges.
But why would that count as lower-level than *** / equals / *** ? I think perhaps because the word "converges" is quite a lot more specific and area-dependent than the word "equals".
Hmm ... I thought writing this was going to be easier than it has turned out to be.
Post new comment
(Note: commenting is not possible on this snapshot.)