This page contains descriptions of a number of groups that can be used as tests for the truth or falsity of general group-theoretic statements.
 |
Cyclic groups
The cyclic group of order  , often denoted by
, often denoted by 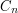 , can be described in various ways. It is the group of all integers mod
, can be described in various ways. It is the group of all integers mod  under addition, or the group of all rotational symmetries of a regular
under addition, or the group of all rotational symmetries of a regular  -gon, or the group of all
-gon, or the group of all  th roots of unity under multiplication. An abstract definition of a cyclic group is that it is generated by one element: that is, a group
th roots of unity under multiplication. An abstract definition of a cyclic group is that it is generated by one element: that is, a group  is cyclic if there is an element
is cyclic if there is an element 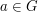 such that every element of
such that every element of  is a power of
is a power of 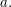
If  is prime, then by Lagrange's theorem the cyclic group of order
is prime, then by Lagrange's theorem the cyclic group of order  has no subgroups apart from two trivial ones: the identity and the whole group. It also follows from Lagrange's theorem that every group of order
has no subgroups apart from two trivial ones: the identity and the whole group. It also follows from Lagrange's theorem that every group of order  is cyclic (since every element
is cyclic (since every element  generates a subgroup, so if
generates a subgroup, so if  is not the identity then that subgroup must be the whole group). Therefore, up to isomorphism there is exactly one group of order
is not the identity then that subgroup must be the whole group). Therefore, up to isomorphism there is exactly one group of order  .
.
Since 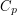 has no non-trivial subgroups, it is in particular a simple group: that is, it has no non-trivial normal subgroups. The groups
has no non-trivial subgroups, it is in particular a simple group: that is, it has no non-trivial normal subgroups. The groups 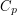 are the only Abelian simple groups.
are the only Abelian simple groups.
The group 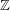 of all integers under addition is cyclic (according to the abstract definition, even if it is shaped more like a line than a circle). It is the only infinite cyclic group. Every subgroup of
of all integers under addition is cyclic (according to the abstract definition, even if it is shaped more like a line than a circle). It is the only infinite cyclic group. Every subgroup of 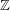 apart from
apart from 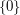 is isomorphic to the whole group.
is isomorphic to the whole group.
Dihedral groups
The dihedral group of order 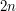 , often denoted by
, often denoted by 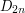 but also, slightly confusingly, often denoted by
but also, slightly confusingly, often denoted by 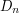 – we shall write
– we shall write 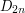 in this article – can be described concretely as the group of all symmetries of a regular
in this article – can be described concretely as the group of all symmetries of a regular  -gon, or abstractly as the group generated by two elements
-gon, or abstractly as the group generated by two elements 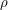 and
and  that satisfy the relations
that satisfy the relations 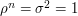 and
and 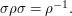 (See presentations of groups if you do not understand the previous sentence.)
(See presentations of groups if you do not understand the previous sentence.)
The dihedral group of order 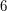 is isomorphic to
is isomorphic to 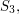 the group of permutations of a set of size
the group of permutations of a set of size 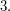 It is the only non-Abelian group of order
It is the only non-Abelian group of order 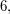 and the smallest non-Abelian group.
and the smallest non-Abelian group.
Dihedral groups are not simple, since the element 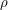 generates a subgroup of index
generates a subgroup of index 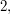 and all subgroups of index
and all subgroups of index 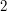 are automatically normal. (It is also easy to see directly that this particular subgroup is normal.)
are automatically normal. (It is also easy to see directly that this particular subgroup is normal.)
Number systems
If you want to know whether there is a group  with a certain property, and
with a certain property, and  is allowed to be infinite, then the most obvious examples to try are
is allowed to be infinite, then the most obvious examples to try are 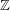 ,
, 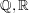 and
and 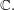 You could also consider taking quotients of these; for example,
You could also consider taking quotients of these; for example, 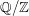 is an infinite torsion group (i.e., every element has finite order).
is an infinite torsion group (i.e., every element has finite order).
The symmetric groups
A permutation of a set  is a bijection from
is a bijection from  to
to 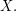 The symmetric group on a set of size
The symmetric group on a set of size  , denoted
, denoted 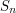 is the group of all permutations of the set
is the group of all permutations of the set 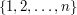 (or of any other set
(or of any other set  of size
of size  if that is more convenient).
if that is more convenient).
Every group of order  is isomorphic to a subgroup of
is isomorphic to a subgroup of 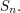 To see this, let
To see this, let  be a group of order
be a group of order  and associate with each element
and associate with each element 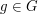 the permutation
the permutation 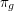 from
from  to
to  that takes
that takes 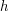 to
to 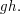 The map
The map 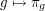 is easily seen to be a homomorphism. Indeed,
is easily seen to be a homomorphism. Indeed, 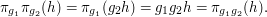
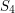 is isomorphic to the group of rotations of a cube (or regular octahedron). A good way to see this is to note that every rotation of the cube permutes the four diagonals of the cube. This gives us a homomorphism from the rotation group of the cube to
is isomorphic to the group of rotations of a cube (or regular octahedron). A good way to see this is to note that every rotation of the cube permutes the four diagonals of the cube. This gives us a homomorphism from the rotation group of the cube to 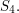 One can check that every rotation that sends each diagonal to itself is the identity, so the kernel of the homomorphism is trivial. Since there are
One can check that every rotation that sends each diagonal to itself is the identity, so the kernel of the homomorphism is trivial. Since there are 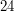 rotations of the cube (each vertex has eight choices of where to go, and each neighbour of that vertex then has three choices of where to go, after which the rotation is determined), the homomorphism is an isomorphism.
rotations of the cube (each vertex has eight choices of where to go, and each neighbour of that vertex then has three choices of where to go, after which the rotation is determined), the homomorphism is an isomorphism.
The alternating groups
The alternating group on a set of size  , denoted
, denoted 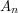 , is the group of all even permutations of the set
, is the group of all even permutations of the set 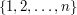 (or, again, of any other set
(or, again, of any other set  of size
of size  ).
).
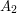 is the trivial group and
is the trivial group and 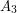 is the cyclic group of order
is the cyclic group of order 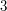 , so the first interesting alternating group is
, so the first interesting alternating group is 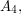 which has order
which has order 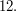 The subgroup of
The subgroup of 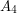 consisting of the identity and the three permutations
consisting of the identity and the three permutations 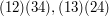 and
and 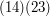 is normal. This follows because if
is normal. This follows because if 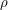 and
and  are permutations, then
are permutations, then 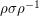 has the same cycle type as
has the same cycle type as  . Therefore, this subgroup is a union of conjugacy classes. However, for
. Therefore, this subgroup is a union of conjugacy classes. However, for 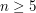 it can be shown that
it can be shown that 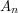 is a simple group: the alternating groups form one of the infinite families of simple groups.
is a simple group: the alternating groups form one of the infinite families of simple groups.
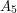 is isomorphic to the group of rotations of a regular dodecahedron. A nice way to see this is to start by observing that the vertices of the dodecahedron can be partitioned into (the vertices of) five regular tetrahedra. Therefore,
is isomorphic to the group of rotations of a regular dodecahedron. A nice way to see this is to start by observing that the vertices of the dodecahedron can be partitioned into (the vertices of) five regular tetrahedra. Therefore, 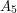 acts on the set of these tetrahedra, which gives us a homomorphism from group of rotations of the dodecahedron to
acts on the set of these tetrahedra, which gives us a homomorphism from group of rotations of the dodecahedron to 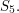 One can show that any rotation that sends each of the five tetrahedra to itself must be the identity, so the kernel of this homomorphism is trivial. It is simple to prove that there are
One can show that any rotation that sends each of the five tetrahedra to itself must be the identity, so the kernel of this homomorphism is trivial. It is simple to prove that there are 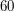 rotations of a dodecahedron (each face can to to one of twelve others, and can be rotated in one of five ways when it gets there), so the rotation group is isomorphic to a subgroup of
rotations of a dodecahedron (each face can to to one of twelve others, and can be rotated in one of five ways when it gets there), so the rotation group is isomorphic to a subgroup of 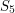 of index
of index 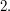 The only such subgroup is
The only such subgroup is 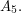
Free groups
The free group on  generators
generators 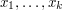 is the group whose elements are all strings
is the group whose elements are all strings 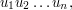 where each
where each 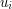 is equal to
is equal to 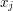 or
or 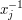 for some
for some 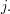 Two such strings are regarded as the same if you can get from one to the other by inserting or deleting pairs of the form
Two such strings are regarded as the same if you can get from one to the other by inserting or deleting pairs of the form 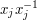 or
or 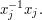 For example, in the free group on the three generators
For example, in the free group on the three generators 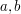 and
and 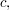 the string
the string 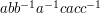 represents the same element as the string
represents the same element as the string 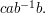
If you are looking for a group generated by  elements and you want it not to have any properties that are not forced on you by the group axioms, then the free group on
elements and you want it not to have any properties that are not forced on you by the group axioms, then the free group on  generators is a good choice. Formally, this is expressed via a universal_property as follows. Let
generators is a good choice. Formally, this is expressed via a universal_property as follows. Let 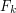 be the free group on the generators
be the free group on the generators 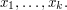 Then, given any group
Then, given any group  and any
and any  elements
elements 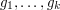 of
of 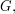 there is a unique homomorphism
there is a unique homomorphism 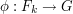 that sends
that sends 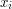 to
to 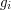 for each
for each 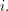 It is not hard to see intuitively why this is true. Indeed, once one has mapped
It is not hard to see intuitively why this is true. Indeed, once one has mapped 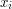 to
to 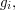 then the rest of
then the rest of 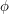 is forced: for example,
is forced: for example, 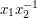 must map to
must map to 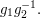 The only thing that is not quite trivial is that different strings that represent the same element of
The only thing that is not quite trivial is that different strings that represent the same element of 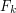 map to the same element of
map to the same element of 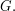 But this follows from the fact that the only equations satisfied by
But this follows from the fact that the only equations satisfied by 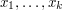 are those guaranteed to hold by the group axioms, which means that they are also satisfied by
are those guaranteed to hold by the group axioms, which means that they are also satisfied by 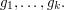
The ''free Abelian group on  generators" is isomorphic to
generators" is isomorphic to 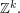 The simplest set of generators of
The simplest set of generators of 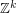 is the standard basis of
is the standard basis of 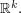 The only equations satisfied by the generators are those guaranteed to hold by the group axioms and commutativity. This too can be expressed as a universal property – just replace "for any group" by "for any Abelian group" in the universal property for the free group
The only equations satisfied by the generators are those guaranteed to hold by the group axioms and commutativity. This too can be expressed as a universal property – just replace "for any group" by "for any Abelian group" in the universal property for the free group 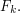 See also the Wikipedia article on free groups.
See also the Wikipedia article on free groups.
Linear groups
Many interesting groups arise as groups of invertible linear maps. An obvious example is the general linear group GL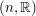 of all invertible linear maps from
of all invertible linear maps from 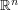 to
to 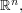 or equivalently of all invertible
or equivalently of all invertible 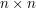 real matrices. There are two ways of modifying this example: one can replace
real matrices. There are two ways of modifying this example: one can replace 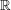 by another field, and one can impose restrictions on the invertible maps. For instance, the special linear group SL
by another field, and one can impose restrictions on the invertible maps. For instance, the special linear group SL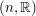 is the group of all
is the group of all 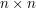 real matrices with determinant
real matrices with determinant 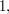 the orthogonal group O(
the orthogonal group O( ) is the group of all real orthogonal matrices, SL
) is the group of all real orthogonal matrices, SL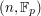 is the group of all
is the group of all 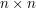 matrices of determinant
matrices of determinant  with elements in the field
with elements in the field 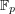 with
with  elements, and so on.
elements, and so on.
The group PSL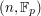 is the quotient of SL
is the quotient of SL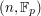 by the subgroup of all scalar multiples of the identity. Except for a few very small values of
by the subgroup of all scalar multiples of the identity. Except for a few very small values of  and
and 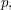 PSL
PSL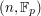 is simple.
is simple.
Linear groups over finite fields tend to have good expansion properties: if you choose a set 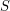 of generators then the size of the set of elements you can form as a product of
of generators then the size of the set of elements you can form as a product of  elements of
elements of 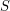 grows rapidly as
grows rapidly as  grows.
grows.
The quaternion group
The quaternion group is a group of order 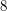 with elements
with elements 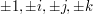 , which satisfy the relations
, which satisfy the relations 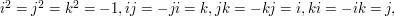 as well as the relations suggested by the notation, such as
as well as the relations suggested by the notation, such as 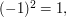
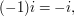 and so on.
and so on.
The quaternion group is non-Abelian (since 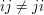 ). It is not isomorphic to
). It is not isomorphic to 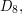 because it has only one element of order
because it has only one element of order 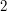 (namely
(namely 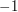 ), whereas
), whereas 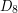 has five (four reflections and a half turn).
has five (four reflections and a half turn).
The Heisenberg group
The Heisenberg group is the group of all 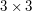 matrices
matrices 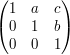 with
with 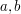 and
and  belonging to
belonging to  The discrete Heisenberg group is the same but with
The discrete Heisenberg group is the same but with 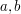 and
and  belonging to
belonging to 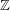 instead.
instead.
The Heisenberg group is non-Abelian, but it is close to Abelian, in the sense that it is 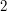 -step nilpotent. The centre of the Heisenberg group is the set of all matrices for which
-step nilpotent. The centre of the Heisenberg group is the set of all matrices for which 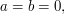 and the quotient by the centre is isomorphic to
and the quotient by the centre is isomorphic to 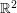 (or
(or 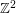 in the discrete case). This makes the Heisenberg group a good group to begin with if one wishes to generalize a result that holds for Abelian groups.
in the discrete case). This makes the Heisenberg group a good group to begin with if one wishes to generalize a result that holds for Abelian groups.
 Tricki
Tricki
Comments
Minimal examples
Wed, 27/05/2009 - 01:56 — Gabe Cunningham (not verified)In the spirit of this page, would it be useful/desirable to have minimal examples of groups with certain properties (or failing to have certain properties?) Another similar idea would be to make a table using several basic group properties (e.g., abelian, simple, finite, torsion) and to give an example group or family of groups for each possible combination of properties. Perhaps such a table would be better served as part of a separate article detailing various nice properties of groups, with crosslinks to and from here. I'd be happy to start such a page if there is interest.
Articles along those kinds of
Sat, 30/05/2009 - 17:41 — gowersArticles along those kinds of lines sound like a great idea to me.
Post new comment
(Note: commenting is not possible on this snapshot.)