Quick description
Transfinite induction is similar to induction but the well-ordered set 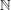 is replaced by larger ordinals. This article tells you what you need to know about ordinals in order to be able to prove results by transfinite induction, gives examples of its use, and distinguishes between various different types of transfinite-induction argument.
is replaced by larger ordinals. This article tells you what you need to know about ordinals in order to be able to prove results by transfinite induction, gives examples of its use, and distinguishes between various different types of transfinite-induction argument.
General discussion
The following facts about ordinals are all you need to know about them in order to carry out proofs by transfinite induction.
-
There is a total ordering,
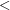 , defined on the class of all ordinals.
, defined on the class of all ordinals. -
0 is an ordinal and there is no smaller ordinal.
-
Given any ordinal
 , the set
, the set 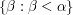 is a well-ordered set.
is a well-ordered set. -
For every set
 there exists a well-ordering of the elements of
there exists a well-ordering of the elements of  . (This is called the well-ordering theorem.)
. (This is called the well-ordering theorem.) -
Given any well-ordered set
 , there is exactly one ordinal
, there is exactly one ordinal  such that
such that  is order-isomorphic to the set
is order-isomorphic to the set 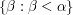 .
. -
Every ordinal
 is either a successor ordinal or a limit ordinal. It is a successor if there is some
is either a successor ordinal or a limit ordinal. It is a successor if there is some  such that
such that  is the smallest ordinal that is greater than
is the smallest ordinal that is greater than  . In this case we write
. In this case we write 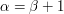 . It is a limit if it is not a successor.
. It is a limit if it is not a successor. -
(Optional, but convenient.) The way ordinals are conventionally constructed,
 is in fact equal to
is in fact equal to 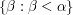 (which implies in particular that
(which implies in particular that 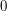 is the empty set). Therefore, instead of talking about the cardinality of
is the empty set). Therefore, instead of talking about the cardinality of 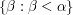 we can talk more simply about the cardinality of
we can talk more simply about the cardinality of  . We can also say that
. We can also say that  is a well-ordered set. The successor of
is a well-ordered set. The successor of  is then
is then 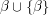 . If
. If  is a limit ordinal, then
is a limit ordinal, then 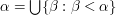 .
. -
(Not needed in proofs, but you ought to know it just to be safe.) Each ordinal is a set, but there is no such thing as the set
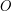 of all ordinals, because if there were then
of all ordinals, because if there were then 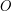 would be an ordinal as well. This is a contradiction since then we would have
would be an ordinal as well. This is a contradiction since then we would have  . However, it is all right to talk about the class of all ordinals.
. However, it is all right to talk about the class of all ordinals. -
Given any set
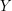 , there is an ordinal
, there is an ordinal  with the same cardinality as
with the same cardinality as 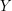 , and hence (since
, and hence (since 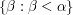 is well-ordered) there is a least such ordinal
is well-ordered) there is a least such ordinal  . Therefore, every set
. Therefore, every set 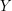 can be well-ordered in such a way that the set of predecessors of any element of
can be well-ordered in such a way that the set of predecessors of any element of 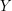 has strictly smaller cardinality than the cardinality of
has strictly smaller cardinality than the cardinality of 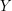 itself.
itself. -
Suppose that we have put a set
 into one-to-one correspondence with an ordinal
into one-to-one correspondence with an ordinal 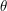 . For each
. For each 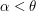 , write
, write 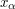 for the element of
for the element of  that corresponds to
that corresponds to  . Suppose that
. Suppose that 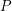 is some statement about elements of
is some statement about elements of  , that
, that 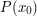 is true, and that
is true, and that  is true whenever
is true whenever 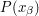 is true for every
is true for every 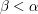 . Then
. Then 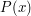 is true for every
is true for every 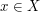 . (This is the principle of transfinite induction.)
. (This is the principle of transfinite induction.)
Example 1
Let us prove that every vector space has a basis. This result is also proved in the article on how to use Zorn's lemma (in a better way).
Let  be a vector space. By the well-ordering theorem, there is a well-ordering of the elements of
be a vector space. By the well-ordering theorem, there is a well-ordering of the elements of  . Therefore, there is an ordinal
. Therefore, there is an ordinal  such that the elements of
such that the elements of  can be put into one-to-one correspondence with
can be put into one-to-one correspondence with  . For each
. For each 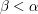 , let us write
, let us write 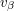 for the element of
for the element of  that corresponds to
that corresponds to  . Now let
. Now let 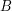 be the set of all
be the set of all 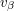 that do not belong to the linear span of their predecessors. It is clear that
that do not belong to the linear span of their predecessors. It is clear that 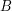 is linearly independent, since if
is linearly independent, since if 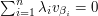 ,
, 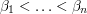 , and
, and 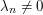 , then we have expressed
, then we have expressed 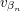 as a linear combination of earlier
as a linear combination of earlier 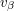 s. It also spans, since every
s. It also spans, since every 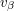 either belongs to
either belongs to 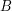 or is a linear combination of earlier elements of
or is a linear combination of earlier elements of 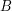 , and every element of
, and every element of  is
is 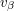 for some
for some  .
.
General discussion
Example 1 might suggest that transfinite induction is just another way of carrying out Zorn's-lemma arguments. And indeed, it can be used for this purpose, but Zorn's lemma is neater and does not require the machinery of ordinals. So Example 1 is not a very good advertisement for the transfinite induction. However, there are situations where transfinite induction really is needed. Typically, these involve a cardinality condition on the initial segments of the well-ordering that one places on the set that one is examining. The next example illustrates this.
Example 2
A famous result of Sierpinski is the existence of a subset  of
of 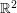 that intersects every line exactly twice. Here is how the proof goes. First, well-order the set of all lines in
that intersects every line exactly twice. Here is how the proof goes. First, well-order the set of all lines in 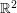 , which has cardinality
, which has cardinality 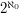 , in such a way that each element has strictly fewer than
, in such a way that each element has strictly fewer than 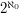 predecessors in the well-ordering. Let
predecessors in the well-ordering. Let 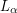 be the line associated with the ordinal
be the line associated with the ordinal  . (If the continuum hypothesis is assumed, then
. (If the continuum hypothesis is assumed, then  must be countable, but we are not assuming the continuum hypothesis.)
must be countable, but we are not assuming the continuum hypothesis.)
We now build up our set  as follows. Suppose that we have found for each
as follows. Suppose that we have found for each 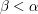 a set
a set 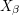 such that for every
such that for every 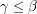 we have
we have 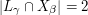 and such that for every line
and such that for every line 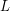 we have
we have 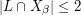 . Suppose also that we have done this in such a way that if
. Suppose also that we have done this in such a way that if  then
then 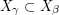 . Finally, suppose that all the sets
. Finally, suppose that all the sets 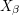 have cardinality strictly less than
have cardinality strictly less than 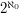 .
.
Let 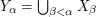 and note that the cardinality of
and note that the cardinality of 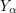 is strictly less than
is strictly less than 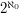 (since for any infinite cardinal
(since for any infinite cardinal  , a union of
, a union of  many sets of size
many sets of size  has size
has size  ). Then
). Then 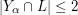 for every line
for every line 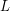 (since otherwise there would have to be some
(since otherwise there would have to be some  such that
such that 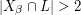 ), and
), and 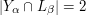 for every
for every 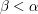 . If
. If 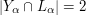 , then let
, then let 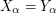 , and the induction has continued to stage
, and the induction has continued to stage  . Otherwise, the number of lines that go through two points of
. Otherwise, the number of lines that go through two points of 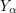 is strictly less than
is strictly less than 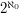 , and each of these lines intersects
, and each of these lines intersects 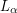 at most once, so we can find infinitely many points in
at most once, so we can find infinitely many points in 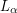 that do not belong to any of those lines. (We want to avoid those intersections since we do not want to have three points of
that do not belong to any of those lines. (We want to avoid those intersections since we do not want to have three points of 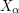 in the same line.) Add either one or two of these points to
in the same line.) Add either one or two of these points to 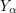 to create
to create 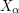 , and again the induction has continued to stage
, and again the induction has continued to stage  .
.
This proves that we can construct sets 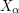 for every
for every  . The union of all these sets
. The union of all these sets 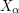 has the property that we want of
has the property that we want of  .
.
General discussion
The big difference between the second argument and the first is that we insisted that each element of the well-ordering had fewer predecessors than the cardinality of the set of all lines, which happened to be the same as the cardinality of each individual line. A cardinality condition such as this gives rise to an argument that cannot be straightforwardly converted into a Zorn's-lemma argument.
Sometimes one needs a stronger cardinality assumption still: one wants the set of all predecessors of any given element to be countable. This requires the continuum hypothesis. The article on how to use the continuum hypothesis has some examples of arguments of this kind.
Example 3
Many interesting uses of transfinite induction use just the countable ordinals (without any assumption that the number of these is 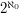 ). As a simple but representative example, let us prove that there is an uncountable collection of well-ordered subsets of
). As a simple but representative example, let us prove that there is an uncountable collection of well-ordered subsets of 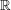 , no two of which are order-isomorphic.
, no two of which are order-isomorphic.
We shall prove this by constructing for each countable ordinal  a well-ordered subset
a well-ordered subset 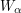 of
of 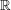 that is order-isomorphic to
that is order-isomorphic to  . This we do using transfinite induction up to (but not including) the first uncountable ordinal. The induction starts with our setting
. This we do using transfinite induction up to (but not including) the first uncountable ordinal. The induction starts with our setting  . Now let
. Now let  be a countable ordinal. As our inductive hypothesis we will take the slightly stronger statement that for every
be a countable ordinal. As our inductive hypothesis we will take the slightly stronger statement that for every 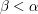 we can choose
we can choose 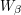 to be a subset of
to be a subset of 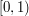 . (But it isn't significantly stronger because
. (But it isn't significantly stronger because 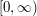 is order-isomorphic to
is order-isomorphic to 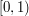 .)
.)
It is convenient to split the proof into the two cases: either  is a successor or
is a successor or  is a limit ordinal. This splitting is a common but not universal feature of transfinite induction arguments over the countable ordinals.
is a limit ordinal. This splitting is a common but not universal feature of transfinite induction arguments over the countable ordinals.
If 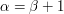 , then the construction of
, then the construction of 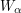 is easy: we just squash
is easy: we just squash 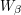 into
into 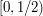 and add an extra point. To be more definite, we can set
and add an extra point. To be more definite, we can set 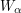 to be
to be 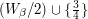 .
.
We now need a small lemma, which is that for every countable limit ordinal  there is an increasing sequence of ordinals
there is an increasing sequence of ordinals 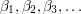 such that
such that 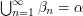 . This is easy to prove. First, enumerate all the ordinals
. This is easy to prove. First, enumerate all the ordinals 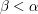 , of which there are countably many. Next, pick a subsequence that consists of every ordinal that is larger than all previous ordinals in the enumeration. This sequence cannot be bounded above by any
, of which there are countably many. Next, pick a subsequence that consists of every ordinal that is larger than all previous ordinals in the enumeration. This sequence cannot be bounded above by any 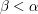 , since there exists
, since there exists 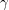 such that
such that 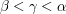 (as
(as  is a limit ordinal), so we would have a contradiction when we got to
is a limit ordinal), so we would have a contradiction when we got to 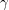 in the enumeration. Therefore, its union is indeed
in the enumeration. Therefore, its union is indeed  (because it contains every
(because it contains every 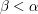 ).
).
Given such a sequence, construct 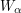 as follows. For each
as follows. For each  , let
, let 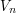 be an order-isomorphic copy of
be an order-isomorphic copy of 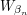 that lives in the interval
that lives in the interval 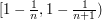 (obtained as a linear image of
(obtained as a linear image of 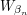 , say). Next, remove from
, say). Next, remove from 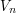 an initial segment that is order-isomorphic to
an initial segment that is order-isomorphic to 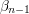 and call this set
and call this set 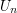 . (To put this loosely, remove the first
. (To put this loosely, remove the first 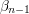 elements of
elements of 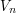 .) Then
.) Then 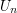 is order-isomorphic to
is order-isomorphic to 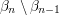 and every element of
and every element of 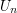 is larger than every element of
is larger than every element of 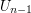 . The union of the sets
. The union of the sets 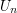 lives in
lives in 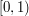 and is order-isomorphic to the union of the sets
and is order-isomorphic to the union of the sets 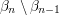 , which equals the union of the sets
, which equals the union of the sets 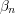 , which equals
, which equals  . Thus, the inductive step is proved.
. Thus, the inductive step is proved.
General discussion
Transfinite induction over the countable ordinals is often used to give a measure of complexity. For example, we could say that the complexity of a well-ordered subset of 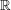 is the unique ordinal that is order-isomorphic to it. Another well-known example is the complexity of Borel sets. We can define open sets and closed sets to have complexity 0, and then say that a set
is the unique ordinal that is order-isomorphic to it. Another well-known example is the complexity of Borel sets. We can define open sets and closed sets to have complexity 0, and then say that a set  has complexity at most
has complexity at most  if it is a countable union or countable intersection of sets
if it is a countable union or countable intersection of sets  such that each
such that each  has complexity at most
has complexity at most 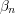 for some
for some 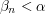 . The complexity of
. The complexity of  is the least ordinal
is the least ordinal  such that
such that  has complexity at most
has complexity at most  . This is a definition by transfinite induction. It is possible to prove, again by transfinite induction, that for every countable ordinal
. This is a definition by transfinite induction. It is possible to prove, again by transfinite induction, that for every countable ordinal  there is a Borel set that has complexity
there is a Borel set that has complexity  . Thus, there are uncountably many different kinds of Borel set.
. Thus, there are uncountably many different kinds of Borel set.
 Tricki
Tricki
Comments
Symbol for total order
Sat, 25/04/2009 - 00:21 — JoseBroxA total order is supposed to be total, in the sense that for every pair
is supposed to be total, in the sense that for every pair  , we have either
, we have either 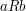 or
or 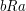 . Choosing the symbol
. Choosing the symbol 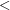 instead of
instead of 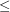 for the total order can be deceptive because it usually means "lesser but not equal". It's clear that this order isn't total, because we don't have
for the total order can be deceptive because it usually means "lesser but not equal". It's clear that this order isn't total, because we don't have 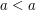 . So, either it is a mistake or it is a conscious choice of the symbol. I haven't changed the notation myself precisely because there could be a good explanation to do it like this. If I don't receive an answer in several days I will change it.
. So, either it is a mistake or it is a conscious choice of the symbol. I haven't changed the notation myself precisely because there could be a good explanation to do it like this. If I don't receive an answer in several days I will change it.
I always thought that a total
Sat, 25/04/2009 - 00:50 — gowersI always thought that a total order could be strict, and that the condition was that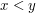 ,
, 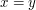 or
or 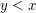 . Is that a very nonstandard convention?
. Is that a very nonstandard convention?
The relation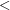 on the ordinals is more convenient to use than
on the ordinals is more convenient to use than 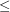 , since one wants many statements to be true for every
, since one wants many statements to be true for every 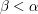 , for some given
, for some given  . I suppose one could add the word "strict" in brackets before the first occurrence of "total order", but that feels a bit strange, given that you can convert orders of the
. I suppose one could add the word "strict" in brackets before the first occurrence of "total order", but that feels a bit strange, given that you can convert orders of the 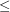 type into orders of the
type into orders of the 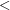 type and back again. Indeed, because of this I describe them both as total orders and think of them as different ways of describing the same basic underlying object.
type and back again. Indeed, because of this I describe them both as total orders and think of them as different ways of describing the same basic underlying object.
You are right
Sat, 25/04/2009 - 01:23 — JoseBroxThat's true, if you ask for the trichotomy law axiom, then both definitions are equivalent. I don't know exactly how nonstandard is this, but since Wikipedia and Planetmath both mention it (Mathworld doesn't!), it should be safe. Maybe in the transfinite context it is more used? (I just checked my copy of Kamke's "Theory of Sets". He uses your convention!).
Excuse me for my comment, I thought the notation was somewhat confusing (but it was more like I was the one confused!)
Post new comment
(Note: commenting is not possible on this snapshot.)