 |
Quick description
One can often use rescaling transformations such as 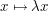 or translation transformations such as
or translation transformations such as 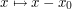 to normalize one or more parameters in the integral to equal a particularly simple value, such as 0 or 1. These changes of variables can create additional factors, but usually such factors can be moved outside of the integral, thus simplifying the remaining integrand.
to normalize one or more parameters in the integral to equal a particularly simple value, such as 0 or 1. These changes of variables can create additional factors, but usually such factors can be moved outside of the integral, thus simplifying the remaining integrand.
Prerequisites
Undergraduate calculus; complex analysis
Example 1
In the integral 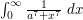 discussed on this page, one can use the substitution
discussed on this page, one can use the substitution 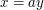 to change this integral to
to change this integral to 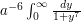 , which in fact already solves the problem except for the task of computing the numerical quantity
, which in fact already solves the problem except for the task of computing the numerical quantity 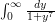 (but if one is willing to lose multiplicative constants, one does not even need to do that, once one checks of course that this quantity is finite).
(but if one is willing to lose multiplicative constants, one does not even need to do that, once one checks of course that this quantity is finite).
Example 2
Problem: (Fourier transform of Gaussians) Compute the integral 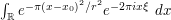 , where
, where 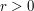 and
and 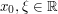 are parameters.
are parameters.
Solution: We begin by using the translation substitution 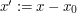 to eliminate the
to eliminate the 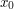 factor:
factor:
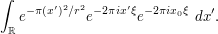
The factor 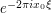 is independent of
is independent of 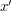 and can be moved out of the integral. Next, we use the scaling substitution
and can be moved out of the integral. Next, we use the scaling substitution 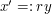 to rewrite the integral as
to rewrite the integral as
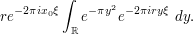
(One could also have used a similar rescaling to eliminate the  factors, but they will turn out to be rather convenient for us, actually, so we will keep them.) The next trick is to complete the square, writing the above integral as
factors, but they will turn out to be rather convenient for us, actually, so we will keep them.) The next trick is to complete the square, writing the above integral as
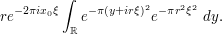
One of the reasons we complete the square is because we can move the 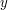 -independent factor out of the integral:
-independent factor out of the integral:
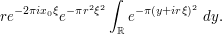
Now we would like to normalize away the 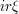 factor by making the substitution
factor by making the substitution 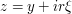 . This turns the real integral into a contour integral, but one should not be afraid of this, and obtain
. This turns the real integral into a contour integral, but one should not be afraid of this, and obtain
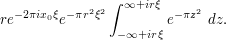
But now we can apply the contour shifting method and get rid of 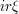 altogether:
altogether:
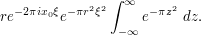
Now we use the standard integral 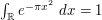 (computed at the square and rearrange page) and arrive at our final answer of
(computed at the square and rearrange page) and arrive at our final answer of 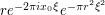 .
.
General discussion
It is often a good tactic to perform as many normalizations as one can first, as this can eliminate many parameters which would otherwise clutter up the arguments later. However, there are exceptions to this rule:
-
Sometimes, one wants to cut up an integral into many pieces, and perform a different normalization for each piece. In such cases, a premature normalization may be counter-productive.
-
In other cases, one wants to do something sneaky with the parameter, e.g. differentiate with respect to it. Again, in that case it may be counter-productive to normalize the parameter prematurely.
One can also use dimensional analysis as a substitute for the rescaling normalisation (examples needed).
 Tricki
Tricki
Comments
Post new comment
(Note: commenting is not possible on this snapshot.)