Quick description
From Fubini's theorem one has the identity
for non-negative  . Thus, to estimate an integral, one way to do this is to control the measure of the level sets
. Thus, to estimate an integral, one way to do this is to control the measure of the level sets 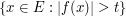 for different values of
for different values of 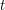 .
.
A slight variant: the 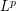 norm of a function
norm of a function  can be expressed by the formula
can be expressed by the formula
As another variant, one can view (1) as a means to decompose any non-negative function  as a superposition of indicator functions:
as a superposition of indicator functions:
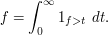
Prerequisites
Measure theory
Example 1
Let 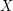 be a finite set, and let
be a finite set, and let 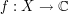 be a function. Show that
be a function. Show that
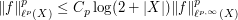
for any 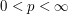 .
.
Solution: we may as well normalize 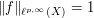 , thus
, thus
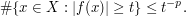
If we insert this bound directly into (2) (using counting measure 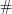 instead of
instead of 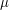 ) we obtain a logarithmic divergence. But we can improve the bound in two ways. Firstly, when
) we obtain a logarithmic divergence. But we can improve the bound in two ways. Firstly, when 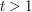 , then
, then 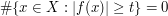 , since there is no other non-negative integer less than
, since there is no other non-negative integer less than 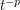 . Secondly, we also have the trivial upper bound of
. Secondly, we also have the trivial upper bound of 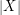 , which is superior when
, which is superior when 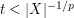 . If we then use "divide and conquer" and partition the integral on the right-hand side of (2) into the regions
. If we then use "divide and conquer" and partition the integral on the right-hand side of (2) into the regions 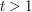 ,
, 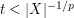 , and
, and 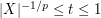 , one obtains the claim.
, one obtains the claim.
Example 2
Show that if a function  lies in the weak
lies in the weak 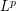 spaces
spaces 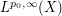 and
and 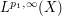 for some measure space
for some measure space 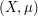 and some exponents
and some exponents 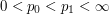 , then it lies in the strong
, then it lies in the strong 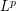 spaces
spaces 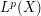 for all
for all 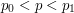 .
.
We need to use "divide and conquer" efficiently in order to 'interpolate' the information we have at the endpoint weak 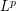 spaces. The idea is that when the function
spaces. The idea is that when the function  is large, say
is large, say 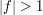 , then the
, then the 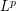 norms increase when
norms increase when 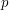 increases which is the same as saying that
increases which is the same as saying that 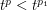 whenever
whenever 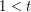 and
and 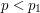 . This indicates that we should split the integral
. This indicates that we should split the integral 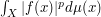 into two parts; one integral over the set where
into two parts; one integral over the set where  is large and one over its complement. Then the integral over the region where
is large and one over its complement. Then the integral over the region where  is large is controlled by the weak
is large is controlled by the weak 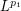 norm of
norm of  and the integral where
and the integral where  is small is controlled by the weak
is small is controlled by the weak 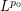 norm of
norm of  .
.
This can be done in a very elegant fashion by using the description (2) of the 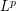 norm of a function. Indeed we can write
norm of a function. Indeed we can write
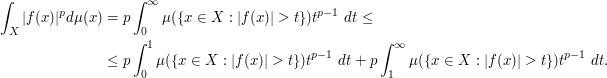
For the first term (which corresponds to the set where  is small) we use the weak
is small) we use the weak 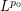 estimate
estimate
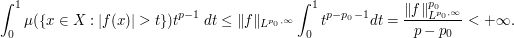
Similarly we get for the second term
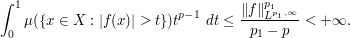
Thus we have
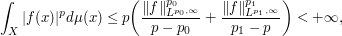
and in particular 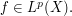
More efficiently, one could split the integral at some point 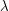 instead of the point
instead of the point 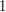 and then optimize in the parameter
and then optimize in the parameter 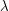 .
.
General discussion
This method is closely related to double counting and "interchange integrals or sums".
The method also combines well with dyadic decomposition. Indeed, one easily verifies that 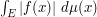 is comparable to
is comparable to 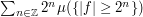 , and more generally
, and more generally 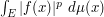 is comparable (up to constants depending on
is comparable (up to constants depending on 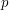 ) to
) to 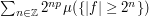 .
.
The Marcinkiewicz interpolation theorem relies heavily on these sorts of level set decompositions.
 Tricki
Tricki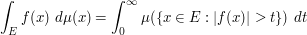
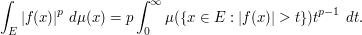
Comments
Post new comment
(Note: commenting is not possible on this snapshot.)