Quick description
When faced with a double integral, such as
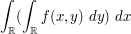
try interchanging the integrals and see if this simplifies the expression. This is good in situations in which  looks easy to integrate in
looks easy to integrate in  but not in
but not in 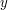 . (See "Which integrals are simpler to integrate".) However, surprisingly often, even if you just interchange the order of integration without thinking in advance what you will get out of it, something good happens.
. (See "Which integrals are simpler to integrate".) However, surprisingly often, even if you just interchange the order of integration without thinking in advance what you will get out of it, something good happens.
Of course, one can similarly interchange sums and integrals, or sums with sums; the latter technique is also known as double counting. The technique is also closely related to linearity of expectation.
Prerequisites
Undergraduate real analysis
Example 1
Let's play around with the Riemann zeta function
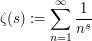
where we restrict attention initially to the case 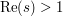 , so there is no difficulty making the sum converge. We will try to expand
, so there is no difficulty making the sum converge. We will try to expand 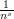 as an integral, so that we can get something interesting by interchanging sums and integrals.
as an integral, so that we can get something interesting by interchanging sums and integrals.
The starting point is the scaling identity
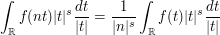
for any  which is bounded and rapidly decreasing. One could try a number of different functions
which is bounded and rapidly decreasing. One could try a number of different functions  here, but a particularly nice one is the Gaussian
here, but a particularly nice one is the Gaussian 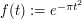 (basically because it is its own Fourier transform). Inserting this, we soon obtain the identity
(basically because it is its own Fourier transform). Inserting this, we soon obtain the identity
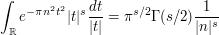
(where 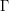 is the Gamma function) so on summing over all non-zero
is the Gamma function) so on summing over all non-zero  and interchanging the integrals we obtain
and interchanging the integrals we obtain
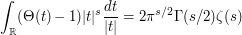
where 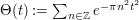 is the Theta function.
is the Theta function.
Now we use the fact that 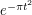 is its own Fourier transform. Combining this with the Poisson summation formula we obtain the identity
is its own Fourier transform. Combining this with the Poisson summation formula we obtain the identity
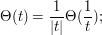
inserting this identity into the above identity (and dividing into the regions 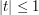 and
and 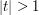 ) we soon arrive at the formula
) we soon arrive at the formula
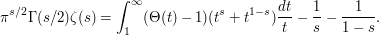
This identity has two important consequences. Firstly, the rapid decay of 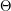 ensures that the right-hand side makes sense for all complex numbers
ensures that the right-hand side makes sense for all complex numbers  (except for the poles at
(except for the poles at 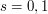 ), and thus explicitly defines a meromorphic continuation of
), and thus explicitly defines a meromorphic continuation of 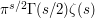 and hence
and hence 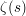 . Secondly, the right-hand side is symmetric with respect to the reflection
. Secondly, the right-hand side is symmetric with respect to the reflection 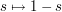 , leading to the celebrated functional equation
, leading to the celebrated functional equation
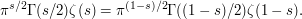
Example 2
(More suggestions welcome!)
General discussion
In order to justify the interchange of integrals, one can use results such as the Fubini-Tonelli theorem. Alternatively, one can create an epsilon of room to regularize, discretize or truncate the integrand to the point where the interchange of integrals can be justified, and then take limits at the end of the argument.
Sometimes it is worthwhile to expand an integrand into a series or integral of other expressions for the sole purpose of applying the interchanging integrals trick. For instance, this is one major motivation for using Fourier identities.
 Tricki
Tricki
Comments
Examples for reversing summation and integration
Thu, 23/04/2009 - 01:42 — Zygmund (not verified)As an example, how about the proof via theta-functions of the functional equation for the Riemann-zeta function (or L-functions)?
Nice suggestion!
Thu, 23/04/2009 - 02:37 — taoI've added it in as an example. More suggestions would of course also be good :)
Another example
Thu, 23/04/2009 - 12:30 — JoseBroxThis one in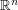 , how to change a
, how to change a  -dimensional
-dimensional 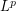 -norm into a 1-dimensional integral:
-norm into a 1-dimensional integral:
(Here the absolute value means the Lebesgue measure)
It is used, for example, to prove Marcinkiewicz's Interpolation Theorem.
The proof of this simple fact is:
where we used Fubini to go from step 2 to step 3.
Post new comment
(Note: commenting is not possible on this snapshot.)