I don't like this first sentence, for two reasons.
1. I disagree with it. I think probability theory is the study of ... probabilities, and probability measures are how we formulate that in a rigorous way. (For example, one would never say, "Number theory is the study of finite sets that are transitive and totally ordered by inclusion." Rather, it's the study of numbers and their relationships, and it so happens that we (sometimes) model numbers with the help of set theory.)
2. It will put off many readers. There will be lots of probability articles on the Tricki that will be comprehensible to someone who knows no measure theory, and they won't all be elementary.
A slightly more subtle objection (to the second paragraph) is that I don't like the identification of random variables with measurable functions. This is a point that was made to me by a probabilist who wrote for the Princeton Companion to Mathematics: almost all the time, one can analyse random variables without having to worry about what sample space one is using, and this is the "correct" way to think probabilistically.
Having said that, there is a place for the view of probability that you are putting forward here – as a sort of branch of measure theory. Perhaps there should be a measure theory front page with a subpage devoted to probability measures.
I'm not making any changes at the moment, partly because of time constraints and partly because others may wish to express their views before I go ahead and do anything.
Yes, you are right; I could have done the changes myself and I usually do this kind of work in Wikis (format/grammar editing). But here we have the luck of being a small site (yet) and I had the opportunity to expose my opinion directly to you and, in case you got convinced of the correctness of the change, I would have saved myself from the need of editing all your articles anytime you didn't use the courtesy plural ;-)
It's just the old topic of teaching how to grow wheat instead of just giving bread, if you allow me the comparison.
From the point of view of linking to this article, it is quite inconvenient to have levels of the hierarchy that are not articles, with sublevels that are. Would it be possible to create small articles for the headings above that are currently in black? (I could do this myself, but am rather busy for the next 24 hours or so.)
My feeling on infinite graphs, for what it's worth, is that they should probably be included here if the graph-theoretical perspective sheds some basic insight on the infinite structure, or if they can give some insight into finite graphs – so the usual graph on might qualify because it does encapsulate many of the properties of grids, but the obvious graph derived from the Leech lattice probably wouldn't qualify, since despite its retaining many of the interesting properties of the Leech lattice, it doesn't actually tell you anything that the lattice itself doesn't already. I'm not really all that familiar with infinite graph theory, though, so I'll probably leave that area mostly alone for now.
I agree with you generally about the organization of the article. I'm a little worried that the boundaries between (2) and the other classes seem kind of nebulous, but that difficulty will probably resolve itself over the course of editing the article.
When I saw the title of this, I thought it might be an amusing article that gave a surprisingly advanced perspective on addition and subtraction, but now I see that it is doing something else. I wonder if a more specific title such as "Add and subtract something simpler" might be an improvement: I think that captures more what the article is about, and also sticks in the mind as a slogan, which is something I hope will happen a lot with the Tricki. (In general, I prefer titles in the form of commands, though I haven't always managed to come up with such titles myself.)
Later: I did in the end go ahead and change the title.
A general comment about the organization of this article. I think I'd suggest something like this.
1. Elementary families of graphs. (Would include complete graphs, complete bipartite graphs, paths, cycles, rooted binary trees, the discrete cube, and probably more.)
2. Elementary graphs derived from other structures. (Would include things like edge-graphs of polyhedra, the usual graph on , and so on.)
3. "Sporadic" graphs with interesting properties, such as the Petersen graph.
Then there are more general ways of coming up with graphs, such as random graphs, Cayley graphs, geometric graphs, interval graphs, etc. (Some of the above graphs can be realized as Cayley graphs, of course, but this doesn't matter.) Here, I think the best thing would be to have a rather brief discussion of what can be done and when one expects these methods to be useful, followed by links to other pages. For example, both random graphs and Cayley graphs are huge topics.
It's not quite clear to me what we should do about infinite graphs. Some infinite graphs, such as the usual graph on , are infinite but not massively different in flavour from finite graphs such as big grids. Others, such as the graph where you well-order the reals and take all pairs such that the usual ordering agrees with the well-ordering, are much more infinitary and probably belong elsewhere.
How about the theorem that ideals are contained in maximal ideals in rings with identities? That seems to be in the same spirit.
Or, the existence of minimal prime ideals.
Instead of saying "I am given..." and "I must show...", I would use the "courtesy plural" and say "We are given..." and "We must show..." as this is the standard rule for scientific writing, If I'm not mistaken ;-)
I've added something about generalized functions, but I'm very far from an expert, so feel free to change it if you don't like it. Actually, now that I've done it I'm starting to think that putting Fourier transforms of hypersurfaces together with Fourier transforms of distributions is not very natural at all, so probably some further work is needed.
I guess one could put all this in the general discussion section (and perhaps divide into subsections). All of these observations are indeed worth putting in the main page. (There will also be some connections with the "control level sets" page and the "linearize the phase" page: making the phase linearisation transformation one sees that the van der Corput integrals are essentially Fourier transforms of the level sets.)
Feel free to make a start on these things; I will try to come back to this page later and add more to it (I'm working my way through various other integration techniques at the moment).
The general principle that sub-level set estimates imply van der Corput type estimates should be somewhere here. Also the nice trick that van der Corput type estimates imply sub-level set estimates would be very useful. However, all these things cannot be under 'Quick description'. Any ideas about how to structure this?
We need a -Fourier transforms of measures and a -Fourier transforms of distributions or you think it should be under the same title? I believe that Fourier transforms of measures deserve a special heading here. But I don't know where to start really. Trying to define Fourier transforms of measures in full generality might be confusing. I would start on the real line or the circle to make things more concrete and simple. Then I would go on defining Fourier transforms of measures in the Euclidean space . I guess some special section should be devoted to measures supported on sub-manifolds of and there should be a chain that connects to curvature and oscillatory integrals. Also a 'Parent' of this article should be ' estimates' but I don't know if there is such an article yet.
How would you feel about changing the title of this to "How to use the Fourier transform" (a title that I had put on the how-to-use wishlist)? Or is this article meant to be more specific, and just concentrating on things where applying a Fourier identity immediately simplifies your problem? In that case, "How to use the Fourier transform" could become a navigation page.
Actually, as I write this I am starting to think that the second idea is obviously better: there are so many uses of the Fourier transform, and so many perspectives on it, that it seems better to have a whole hierarchy of pages about it. Also, the top of this hierarchy might more appropriately be called "Fourier transforms front page". So what I'll do for now is create a Fourier transforms front page, which will be the page you get to when you click on "How to use the Fourier transform". And I'll make that a second parent of this article. If people don't like these decisions, they aren't set in stone.
It would be better to give this article a more specific name, and place it into a hierarchy under the Differential equations front page. In particular "simple" is not a well-defined term here. Presumably "linear" is what is meant, and furthermore a better discussion of linearity should be given, in order to motivate the separation into "homogeneous" and "particular" solutions.
True, but I just feel that fact should be mentioned somewhere in the article - if only as a sidenote.
I'm merely worried someone relatively new to the issue of countability may think finiteness is *required*. Perhaps a note in parentheses at the end of the paragraph stating that countably infinite inverses work as well, but it's usually more appropriate/easier to find a finite case?
I don't like this first sentence, for two reasons.
1. I disagree with it. I think probability theory is the study of ... probabilities, and probability measures are how we formulate that in a rigorous way. (For example, one would never say, "Number theory is the study of finite sets that are transitive and totally ordered by inclusion." Rather, it's the study of numbers and their relationships, and it so happens that we (sometimes) model numbers with the help of set theory.)
2. It will put off many readers. There will be lots of probability articles on the Tricki that will be comprehensible to someone who knows no measure theory, and they won't all be elementary.
A slightly more subtle objection (to the second paragraph) is that I don't like the identification of random variables with measurable functions. This is a point that was made to me by a probabilist who wrote for the Princeton Companion to Mathematics: almost all the time, one can analyse random variables without having to worry about what sample space one is using, and this is the "correct" way to think probabilistically.
Having said that, there is a place for the view of probability that you are putting forward here – as a sort of branch of measure theory. Perhaps there should be a measure theory front page with a subpage devoted to probability measures.
I'm not making any changes at the moment, partly because of time constraints and partly because others may wish to express their views before I go ahead and do anything.
Yes, you are right; I could have done the changes myself and I usually do this kind of work in Wikis (format/grammar editing). But here we have the luck of being a small site (yet) and I had the opportunity to expose my opinion directly to you and, in case you got convinced of the correctness of the change, I would have saved myself from the need of editing all your articles anytime you didn't use the courtesy plural ;-)
It's just the old topic of teaching how to grow wheat instead of just giving bread, if you allow me the comparison.
From the point of view of linking to this article, it is quite inconvenient to have levels of the hierarchy that are not articles, with sublevels that are. Would it be possible to create small articles for the headings above that are currently in black? (I could do this myself, but am rather busy for the next 24 hours or so.)
My feeling on infinite graphs, for what it's worth, is that they should probably be included here if the graph-theoretical perspective sheds some basic insight on the infinite structure, or if they can give some insight into finite graphs – so the usual graph on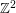 might qualify because it does encapsulate many of the properties of grids, but the obvious graph derived from the Leech lattice probably wouldn't qualify, since despite its retaining many of the interesting properties of the Leech lattice, it doesn't actually tell you anything that the lattice itself doesn't already. I'm not really all that familiar with infinite graph theory, though, so I'll probably leave that area mostly alone for now.
might qualify because it does encapsulate many of the properties of grids, but the obvious graph derived from the Leech lattice probably wouldn't qualify, since despite its retaining many of the interesting properties of the Leech lattice, it doesn't actually tell you anything that the lattice itself doesn't already. I'm not really all that familiar with infinite graph theory, though, so I'll probably leave that area mostly alone for now.
I agree with you generally about the organization of the article. I'm a little worried that the boundaries between (2) and the other classes seem kind of nebulous, but that difficulty will probably resolve itself over the course of editing the article.
I will change this, but as I understand the way a wiki works, you could have changed it yourself. The author doesn't own the article.
This one in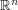 , how to change a
, how to change a  -dimensional
-dimensional 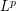 -norm into a 1-dimensional integral:
-norm into a 1-dimensional integral:
(Here the absolute value means the Lebesgue measure)
It is used, for example, to prove Marcinkiewicz's Interpolation Theorem.
The proof of this simple fact is:
where we used Fubini to go from step 2 to step 3.
When I saw the title of this, I thought it might be an amusing article that gave a surprisingly advanced perspective on addition and subtraction, but now I see that it is doing something else. I wonder if a more specific title such as "Add and subtract something simpler" might be an improvement: I think that captures more what the article is about, and also sticks in the mind as a slogan, which is something I hope will happen a lot with the Tricki. (In general, I prefer titles in the form of commands, though I haven't always managed to come up with such titles myself.)
Later: I did in the end go ahead and change the title.
A general comment about the organization of this article. I think I'd suggest something like this.
1. Elementary families of graphs. (Would include complete graphs, complete bipartite graphs, paths, cycles, rooted binary trees, the discrete cube, and probably more.)
2. Elementary graphs derived from other structures. (Would include things like edge-graphs of polyhedra, the usual graph on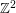 , and so on.)
, and so on.)
3. "Sporadic" graphs with interesting properties, such as the Petersen graph.
Then there are more general ways of coming up with graphs, such as random graphs, Cayley graphs, geometric graphs, interval graphs, etc. (Some of the above graphs can be realized as Cayley graphs, of course, but this doesn't matter.) Here, I think the best thing would be to have a rather brief discussion of what can be done and when one expects these methods to be useful, followed by links to other pages. For example, both random graphs and Cayley graphs are huge topics.
It's not quite clear to me what we should do about infinite graphs. Some infinite graphs, such as the usual graph on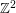 , are infinite but not massively different in flavour from finite graphs such as big grids. Others, such as the graph where you well-order the reals and take all pairs
, are infinite but not massively different in flavour from finite graphs such as big grids. Others, such as the graph where you well-order the reals and take all pairs 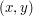 such that the usual ordering agrees with the well-ordering, are much more infinitary and probably belong elsewhere.
such that the usual ordering agrees with the well-ordering, are much more infinitary and probably belong elsewhere.
You can also add trees and forests, and complete bipartite graphs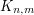 . Maybe pseudoforests and cycle graphs could be interesting too.
. Maybe pseudoforests and cycle graphs could be interesting too.
That's just if we don't want to enter the realm of possibly infinite directed multigraphs with loops ;P
I've added it in as an example. More suggestions would of course also be good :)
How about the theorem that ideals are contained in maximal ideals in rings with identities? That seems to be in the same spirit.
Or, the existence of minimal prime ideals.
As an example, how about the proof via theta-functions of the functional equation for the Riemann-zeta function (or L-functions)?
"either is already small, in which case one can hope that the total contribution of this term is already small" sounds a bit strange to me! :D
is already small, in which case one can hope that the total contribution of this term is already small" sounds a bit strange to me! :D
Instead of saying "I am given..." and "I must show...", I would use the "courtesy plural" and say "We are given..." and "We must show..." as this is the standard rule for scientific writing, If I'm not mistaken ;-)
I've added something about generalized functions, but I'm very far from an expert, so feel free to change it if you don't like it. Actually, now that I've done it I'm starting to think that putting Fourier transforms of hypersurfaces together with Fourier transforms of distributions is not very natural at all, so probably some further work is needed.
I guess one could put all this in the general discussion section (and perhaps divide into subsections). All of these observations are indeed worth putting in the main page. (There will also be some connections with the "control level sets" page and the "linearize the phase" page: making the phase linearisation transformation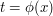 one sees that the van der Corput integrals are essentially Fourier transforms of the level sets.)
one sees that the van der Corput integrals are essentially Fourier transforms of the level sets.)
Feel free to make a start on these things; I will try to come back to this page later and add more to it (I'm working my way through various other integration techniques at the moment).
The general principle that sub-level set estimates imply van der Corput type estimates should be somewhere here. Also the nice trick that van der Corput type estimates imply sub-level set estimates would be very useful. However, all these things cannot be under 'Quick description'. Any ideas about how to structure this?
yannis
We need a -Fourier transforms of measures and a -Fourier transforms of distributions or you think it should be under the same title? I believe that Fourier transforms of measures deserve a special heading here. But I don't know where to start really. Trying to define Fourier transforms of measures in full generality might be confusing. I would start on the real line or the circle to make things more concrete and simple. Then I would go on defining Fourier transforms of measures in the Euclidean space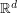 . I guess some special section should be devoted to measures supported on sub-manifolds of
. I guess some special section should be devoted to measures supported on sub-manifolds of 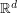 and there should be a chain that connects to curvature and oscillatory integrals. Also a 'Parent' of this article should be '
and there should be a chain that connects to curvature and oscillatory integrals. Also a 'Parent' of this article should be '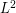 estimates' but I don't know if there is such an article yet.
estimates' but I don't know if there is such an article yet.
yannis
It would be good to have different perspectives on this.
I've now started an article I had planned called If your problem can be expressed in terms of convolutions and inner products then take the Fourier transform. There might be some sense in putting the additive quadruples example there, as it makes a natural first example. Or it could be both there and here. The justification for having both that article and this one (possibly overlapping) is that that one naturally links from the additive combinatorics front page and this one naturally links from estimating integrals.
How would you feel about changing the title of this to "How to use the Fourier transform" (a title that I had put on the how-to-use wishlist)? Or is this article meant to be more specific, and just concentrating on things where applying a Fourier identity immediately simplifies your problem? In that case, "How to use the Fourier transform" could become a navigation page.
Actually, as I write this I am starting to think that the second idea is obviously better: there are so many uses of the Fourier transform, and so many perspectives on it, that it seems better to have a whole hierarchy of pages about it. Also, the top of this hierarchy might more appropriately be called "Fourier transforms front page". So what I'll do for now is create a Fourier transforms front page, which will be the page you get to when you click on "How to use the Fourier transform". And I'll make that a second parent of this article. If people don't like these decisions, they aren't set in stone.
It would be better to give this article a more specific name, and place it into a hierarchy under the Differential equations front page. In particular "simple" is not a well-defined term here. Presumably "linear" is what is meant, and furthermore a better discussion of linearity should be given, in order to motivate the separation into "homogeneous" and "particular" solutions.
Thanks!
OK, I've now added a paragraph making this point but without compromising the theme of the article.
True, but I just feel that fact should be mentioned somewhere in the article - if only as a sidenote.
I'm merely worried someone relatively new to the issue of countability may think finiteness is *required*. Perhaps a note in parentheses at the end of the paragraph stating that countably infinite inverses work as well, but it's usually more appropriate/easier to find a finite case?