Here is a point which I feel needs to be emphasized more in Example 3.
If we try to make the argument work without leaving to be optimized later, but by, say, initially setting , the argument will fail: we will get a useless bound. The reason: we need to pick a function which will grow rapidly while will grow slowly. In this case, grows pretty fast with .
What kind of functions work for this? Well, works: out of the terms in , almost all have expectation . Similarly, works fine as well: in the sum , we will be able to easily cancel many terms because they have expectation .
The central insight behind the proof in Example 3 is that picking for really, really small works. The reason: the average of and is really close to . That is: near one, inversion is about the same as subtraction. This insight can be pushed a little further to argue that if has mean , the quantity should be pretty close to . Thus one might hope that grows slowly - after all, it is "approximately" .
Maybe it'd be nice to mention that if your space is being decomposed into U and V and these have non-empty intersection, then the end terms (H_0 and such) can be taken as reduced homology instead of just normal homology, simplifying some calculations.
If I recall correctly, the Mayer-Vietoris sequence tells you something about a space decomposed as two sets _whose interiors cover the space_. So I think U and V must intersect in two intervals (which are homotopically trivial, so the rest of the proof runs the same).
I would suggest using the less eponymous term "Shatter function lemma" (that Matousek uses in his Lectures on Discrete Geometry) in addition to "Sauer-Shelah lemma". I personally have known this lemma for a long time, but always under the more descriptive name "Shatter function lemma".
Marius Overholt (not verified)10 years 45 weeks agoSmoothing sums
It was actually Waclaw Sierpinski who obtained the exponent 1/3 in the Gauss circle problem, as part of his doctoral dissertation, and who published the result in 1906 (in Polish). His adviser Georgy Voronoi had obtained the same exponent in the Dirichlet divisor problem in 1903. There is an article by Andrzej Schinzel about Sierpinski's papers in number theory in volume XXI of Acta Mathematica (1972). Also there is supposed to exist (but which I have never seen) a description of Sierpinski's proof in German, possibly in some Jahrbuch der Deutsche Mathematikerverein from those years. Schinzel states that the proof is by Voronoi's geometric method. That would mean that the circle is approximated by a polygon, and Euler-Maclaurin summation applied on each piece.
In Proof of Theorem 2:
... use Theorem 1 to identify \mathrm{Hom}_{k(G)}(U,U \otimes_k V) with V (not U),
we see that we may regard S as a subspace of V (not U).
Beyond this, a very nice article.
I don't find the article unintelligible at all; perhaps you could clarify what you find problematic.
Also, editing a page to correct typos (like the missing coefficient you spotted) is very simple: just click on edit at the top of the article. I've corrected it here.
This should probably be restructured to match the form of the articles under "What kind of problem am I trying to solve?". I might even do so myself if I have the time and energy...
This describes one of the most fundamental and general mathematical techniques there is, one so basic that probably most math majors find it second nature already. As such, the description of it as a general technique may be most useful for lower-level pedagogy; failing to grasp this general technique can make math very hard for primary and secondary school students. However, I would love to have examples of its use at all levels and fields, since it is so general-purpose.
My personal favorite way of understanding cubics is the following. In analogy to quadratic equations, try a solution of the form u + v, figuring once we get a single root we can get the other two in short order. Then get rid of the bx^2 term like you did, obtaining x^3 + cx + d = 0. The idea now is to cancel the cx term too. Namely, x^3 = u^3 + 3uv(u + v) + v^3, and cx = c(u + v), so to cancel the cx
term and the 3uv(u + v) term at the same time one stipulates that 3uv = -c.
As a result, one has two equations now: u^3 + v^3 + d = 0, and 3uv = -c. Plugging
v = -c/3u into the first equation gives a quadratic equation in u^3, which has
six solutions u. To each of these three is a single v = -c/3u that works and then one obtains six solutions u + v. But of course u and v are symmetric here so we really just have 3 solutions.
I don't think one really needs to apply the axiom of choice in this context: Since the multifunction is taking values in positive integers, we could just define the corresponding function by taking its value to be the least member of the set of values of the multifunciton. (This process will then, I guess, secretly take us back to the original function construction, where we write each rational in lowest terms — but we don't need to pay attention to this if we don't want to.)
There is a typo in the second paragraph of section Example 1, continued: one should cancel the symbol in the two occurrences of
the expected value of given that
And, reading the last paragraph of this section, I wondered why you picked as an example of extremely unlikely deviation. First, would already yield a rather respectable (i.e., small) bound, namely, something like . Second, there is nothing specific about here, although the formulation seems to indicate otherwise: you might want to add a for example somewhere.
Does it mean the re-write needed to see "variance" is small? Or is it because "partition" naturally suggests "statistics"?
There are reasons to prefer habitually testing for Cauchy-Schwartz, or even Jensen's inequality: for instance they are both more flexible than "variance".
"Think about the converse" should be added as a link in this article.
Here is a point which I feel needs to be emphasized more in Example 3.
If we try to make the argument work without leaving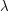 to be optimized later, but by, say, initially setting
to be optimized later, but by, say, initially setting 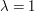 , the argument will fail: we will get a useless bound. The reason: we need to pick a function
, the argument will fail: we will get a useless bound. The reason: we need to pick a function 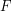 which will grow rapidly while
which will grow rapidly while 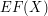 will grow slowly. In this case,
will grow slowly. In this case,  grows pretty fast with
grows pretty fast with  .
.
What kind of functions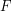 work for this? Well,
work for this? Well, 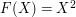 works: out of the
works: out of the 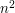 terms in
terms in 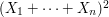 , almost all have expectation
, almost all have expectation 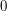 . Similarly,
. Similarly, 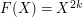 works fine as well: in the sum
works fine as well: in the sum 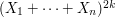 , we will be able to easily cancel many terms because they have expectation
, we will be able to easily cancel many terms because they have expectation 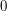 .
.
The central insight behind the proof in Example 3 is that picking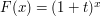 for really, really small
for really, really small 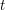 works. The reason: the average of
works. The reason: the average of 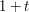 and
and 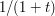 is really close to
is really close to  . That is: near one, inversion is about the same as subtraction. This insight can be pushed a little further to argue that if
. That is: near one, inversion is about the same as subtraction. This insight can be pushed a little further to argue that if  has mean
has mean 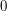 , the quantity
, the quantity  should be pretty close to
should be pretty close to  . Thus one might hope that
. Thus one might hope that ![E[(1+t)^{X_1 + \cdots X_n}] = (E[(1+t)^{X_1}])^n](../images/tex/0679add825aca3c999f44925d38610b4.png) grows slowly - after all, it is "approximately"
grows slowly - after all, it is "approximately" 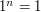 .
.
Maybe it'd be nice to mention that if your space is being decomposed into U and V and these have non-empty intersection, then the end terms (H_0 and such) can be taken as reduced homology instead of just normal homology, simplifying some calculations.
If I recall correctly, the Mayer-Vietoris sequence tells you something about a space decomposed as two sets _whose interiors cover the space_. So I think U and V must intersect in two intervals (which are homotopically trivial, so the rest of the proof runs the same).
what is uv?
I would suggest using the less eponymous term "Shatter function lemma" (that Matousek uses in his Lectures on Discrete Geometry) in addition to "Sauer-Shelah lemma". I personally have known this lemma for a long time, but always under the more descriptive name "Shatter function lemma".
It should be Acta Arithmetica, of course!
It was actually Waclaw Sierpinski who obtained the exponent 1/3 in the Gauss circle problem, as part of his doctoral dissertation, and who published the result in 1906 (in Polish). His adviser Georgy Voronoi had obtained the same exponent in the Dirichlet divisor problem in 1903. There is an article by Andrzej Schinzel about Sierpinski's papers in number theory in volume XXI of Acta Mathematica (1972). Also there is supposed to exist (but which I have never seen) a description of Sierpinski's proof in German, possibly in some Jahrbuch der Deutsche Mathematikerverein from those years. Schinzel states that the proof is by Voronoi's geometric method. That would mean that the circle is approximated by a polygon, and Euler-Maclaurin summation applied on each piece.
In Proof of Theorem 2:
... use Theorem 1 to identify \mathrm{Hom}_{k(G)}(U,U \otimes_k V) with V (not U),
we see that we may regard S as a subspace of V (not U).
Beyond this, a very nice article.
Very good but it would be nice if variable seperation method would be included.
I don't find the article unintelligible at all; perhaps you could clarify what you find problematic.
Also, editing a page to correct typos (like the missing coefficient you spotted) is very simple: just click on edit at the top of the article. I've corrected it here.
This article is unintelligible.
How can it be possible to transform the method of completing the square into such a "charabia".
By the way, a(x+x_0)^2 = ax^2 + 2ax x_0 + x_0^2 is false.
This should probably be restructured to match the form of the articles under "What kind of problem am I trying to solve?". I might even do so myself if I have the time and energy...
This describes one of the most fundamental and general mathematical techniques there is, one so basic that probably most math majors find it second nature already. As such, the description of it as a general technique may be most useful for lower-level pedagogy; failing to grasp this general technique can make math very hard for primary and secondary school students. However, I would love to have examples of its use at all levels and fields, since it is so general-purpose.
Blech, yes, I got stuff reversed. Fixing.
It's a Wiki. Usual advice is to rewrite the style yourself. :-)
My personal favorite way of understanding cubics is the following. In analogy to quadratic equations, try a solution of the form u + v, figuring once we get a single root we can get the other two in short order. Then get rid of the bx^2 term like you did, obtaining x^3 + cx + d = 0. The idea now is to cancel the cx term too. Namely, x^3 = u^3 + 3uv(u + v) + v^3, and cx = c(u + v), so to cancel the cx
term and the 3uv(u + v) term at the same time one stipulates that 3uv = -c.
As a result, one has two equations now: u^3 + v^3 + d = 0, and 3uv = -c. Plugging
v = -c/3u into the first equation gives a quadratic equation in u^3, which has
six solutions u. To each of these three is a single v = -c/3u that works and then one obtains six solutions u + v. But of course u and v are symmetric here so we really just have 3 solutions.
For consistency I've now decided to use \chi throughout that section.
Before (1), the equation for the Fourier transform has \chi when it should have \xi.
I don't think one really needs to apply the axiom of choice in this context: Since the multifunction is taking values in positive integers, we could just define the corresponding function by taking its value to be the least member of the set of values of the multifunciton. (This process will then, I guess, secretly take us back to the original function construction, where we write each rational in lowest terms — but we don't need to pay attention to this if we don't want to.)
This article is should not be part of the Tricki.
I like how you snuck in the Axiom of Choice here, and hid it under the rug since its use is "clear".
Should "difficult" be changed to "easy"?
There is a typo in the second paragraph of section Example 1, continued: one should cancel the symbol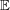 in the two occurrences of
in the two occurrences of
the expected value of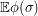 given that
given that
And, reading the last paragraph of this section, I wondered why you picked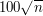 as an example of extremely unlikely deviation. First,
as an example of extremely unlikely deviation. First, 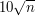 would already yield a rather respectable (i.e., small) bound, namely, something like
would already yield a rather respectable (i.e., small) bound, namely, something like 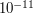 . Second, there is nothing specific about
. Second, there is nothing specific about 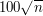 here, although the formulation seems to indicate otherwise: you might want to add a for example somewhere.
here, although the formulation seems to indicate otherwise: you might want to add a for example somewhere.
Thank you for this article.
Does it mean the re-write needed to see "variance" is small? Or is it because "partition" naturally suggests "statistics"?
There are reasons to prefer habitually testing for Cauchy-Schwartz, or even Jensen's inequality: for instance they are both more flexible than "variance".