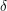This is an attempt to give a quick guide to the top few levels of the Tricki. It may cease to be feasible when the Tricki gets bigger, but we might perhaps be able to automate additions to it. Clicking on arrows just to the right of the name of an article reveals its subarticles. If you want to hide the subarticles again, then you should click to the right of them rather than clicking on the name of one of the subarticles themselves, since otherwise you will follow a link to that subarticle.
What kind of problem am I trying to solve?
 random bits into the structure you want, with the correct distribution. For example, to choose a random graph one can just pick each edge independently at random with probability 1/2. However, a trivial direct approach like this is often not possible: how, for example, would you choose a (labelled) tree uniformly at random? A commonly used technique in more difficult situations is to take a random walk through the "space" of all objects of interest and to prove that the walk is rapidly mixing, which means that after not too long the distribution of where the walk has reached is approximately uniform. )
random bits into the structure you want, with the correct distribution. For example, to choose a random graph one can just pick each edge independently at random with probability 1/2. However, a trivial direct approach like this is often not possible: how, for example, would you choose a (labelled) tree uniformly at random? A commonly used technique in more difficult situations is to take a random walk through the "space" of all objects of interest and to prove that the walk is rapidly mixing, which means that after not too long the distribution of where the walk has reached is approximately uniform. )
- How to solve linear equations in one variable Brief summary ( These are equations like
 . This equation is called linear because the graph of
. This equation is called linear because the graph of 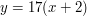 is a straight line. )
is a straight line. ) - How to solve linear equations in two variables Brief summary ( Things get slightly more complicated if you have two unknowns, and two equations to help you to determine them. For example, the equations could be
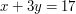 and
and 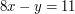 . However, there are various systematic ways of solving such pairs of equations and determining
. However, there are various systematic ways of solving such pairs of equations and determining  and
and 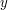 . )
. ) - How to solve linear equations in many variables Brief summary ( The methods used to solve linear equations in two variables can be generalized to any number of variables. At this point it becomes fruitful to think of the unknown as a vector rather than as a sequence of many individual variables. )
- How to solve quadratic equations Brief summary ( A quadratic equation is something like
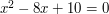 , which involves
, which involves 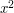 as well as
as well as  . There are several techniques for solving them: which is best varies from example to example. )
. There are several techniques for solving them: which is best varies from example to example. ) - How to solve cubic and quartic equations Brief summary ( These are like quadratic equations, but now they also involve cubes and fourth powers, respectively. For instance, the equation
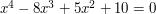 is a quartic equation. Cubic and quartic equations can be solved systematically, but they are much harder than quadratic equations. )
is a quartic equation. Cubic and quartic equations can be solved systematically, but they are much harder than quadratic equations. ) - What makes some equations so much easier to solve than others? Brief summary ( There are several answers one might give to this question but here is one: if you can work something out on your calculator without using any memory, then the resulting equation will be easy to solve. A few examples will make clear what this means. )
- How to solve polynomial equations in several variables
- How to solve linear Diophantine equations
- How to solve quadratic Diophantine equations
- Diophantine equations front page
- Differential equations front page
- How to solve functional equations
- Organized by methods of proof:
- Technique 1: off-the-shelf examples
- Examples of functions defined on the complex numbers
- Examples of functions defined on the real numbers
- Some useful examples of graphs
- Basic examples of groups
- Some examples of manifolds
- Examples and counterexamples in metric spaces
- Some important classes of polynomials
- Some interesting sets of integers
- Some interesting sets of real numbers
- Examples of rings
- Some important solutions of differential equations
- Examples and counterexamples in topological spaces
- How to use Zorn's lemma Brief summary (If you are building a mathematical object in stages and find that (i) you have not finished even after infinitely many stages, and (ii) there seems to be nothing to stop you continuing to build, then Zorn's lemma may well be able to help you.)
- Just-do-it proofs Brief summary (If you are asked to prove that a sequence or a set exists with certain properties, then the best way of doing so may well be just to go ahead and do it: that is, you build the set/sequence up one element at a time, and however you do it you find that it is never difficult to continue building.)
- Turning groups into algebras
- Turning topological spaces into algebras
- Using ordinals to build Banach spaces
- Algebraic constructions of graphs
- Geometrical constructions of graphs
- Building manifolds using polynomials
- Algebraic constructions of sets of integers with given properties
- Building topological spaces out of groups
- Just-do-it proofs
- How to use Zorn's lemma Brief summary (If you are building a mathematical object in stages and find that (i) you have not finished even after infinitely many stages, and (ii) there seems to be nothing to stop you continuing to build, then Zorn's lemma may well be able to help you.)
- Transfinite induction
- How to use the continuum hypothesis
- Finding small nets
- Probabilistic combinatorics front page
- Technique 1: proving that two polynomials are the same by looking at the roots of their difference
- Technique 2: double counting
- Technique 3: using the law of trichotomy
- Technique 4: Axiomatics
- Technique 5: To prove that two objects are equal, show that in enough circumstances they behave in the same way
- Methods:
- Method 1: Convert "every
 " into a single arbitrary
" into a single arbitrary 
- Method 2: Induction
- Method 3: Classification
- Method 4: Prove the result for some cases and deduce it for the rest
General problem-solving tips
Front pages for different areas of mathematics
 , try to realize
, try to realize  as the fundamental group of a topological space. This works best when
as the fundamental group of a topological space. This works best when  is infinite and discrete, especially if
is infinite and discrete, especially if  is finitely presented and torsion-free.)
is finitely presented and torsion-free.)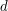 , where the line lies on the surface), but thought of itself as a variety. Since the incidence variety is a set of ordered pairs, it admits two natural projections, onto the first or second member of each ordered pair. Playing off the information that one obtains from considering these two projections, it is often possible to make non-trivial deductions.)
, where the line lies on the surface), but thought of itself as a variety. Since the incidence variety is a set of ordered pairs, it admits two natural projections, onto the first or second member of each ordered pair. Playing off the information that one obtains from considering these two projections, it is often possible to make non-trivial deductions.) is a closed bounded subset of
is a closed bounded subset of 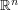 then every sequence in
then every sequence in  has a subsequence that converges to a point in
has a subsequence that converges to a point in  . This article is not so much about the statement, or its proof, but about how to use it in applications. If you come across a statement of a certain form (explained in the article), then the Bolzano-Weierstrass theorem may well be helpful. )
. This article is not so much about the statement, or its proof, but about how to use it in applications. If you come across a statement of a certain form (explained in the article), then the Bolzano-Weierstrass theorem may well be helpful. )
- What is the probabilistic method and when can it be applied?
- Useful heuristic principles for guessing probabilistic estimates
- Unusual choices of probability distribution
- Averaging arguments
- The second-moment method
- How to use martingales
- How to use the Lovász local lemma
- How to use Talagrand's inequality
- How to use Janson's inequality
- Stein's method
- How to use correlation inequalities
- How to use the inclusion-exclusion principle
- Elementary probability
- Use linearity of expectation
- Use the fact that the variances of independent random variables add together
- Bounding probabilities by expectations
- One way of working out the probability of a conjunction of dependent events
- How to use the inclusion-exclusion formula
- Condition on the first thing that happens
- Don't forget the law of total probability
- How to use Bayes's theorem
- How to reason with conditional expectations
How to use mathematical concepts and statements
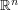 is sequentially compact. More generally, compact metric spaces are sequentially compact. These facts have many applications. Also, some useful diagonalization techniques can be interpreted as saying that certain topological spaces are sequentially compact – as a result, one often hears the phrase "by compactness" when no topology has been specifically mentioned. )
is sequentially compact. More generally, compact metric spaces are sequentially compact. These facts have many applications. Also, some useful diagonalization techniques can be interpreted as saying that certain topological spaces are sequentially compact – as a result, one often hears the phrase "by compactness" when no topology has been specifically mentioned. )
 Tricki
Tricki